Ejercicios resueltos
: Primera ley del movimiento
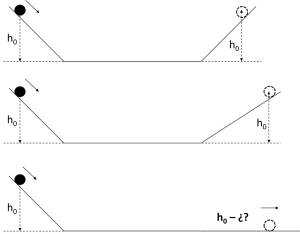
Galileo observó que una bola dejada caer desde cierta altura tiende a subir hasta alcanzar su altura original, sin tener en cuenta la pendiente del plano inclinado. Razonó entonces que, con pendiente cero, la altura inicial nunca se alcanzará.
a) ¿Cómo sería, por tanto, el movimiento sobre un plano horizontal, de acuerdo a estos razonamientos de Galileo?
b) ¿Cómo podría en la práctica lograrse esto?
Análisis, solución y respuestas:
Si la bola tiende a subir por el plano hasta alcanzar la altura inicial desde la que fue lanzada, independientemente de la pendiente que tenga el plano, Galileo razonó que al lanzar una bola por una superficie horizontal esta, una vez iniciado el movimiento, conservaría el valor de su velocidad, y se movería sin detenerse porque no llegaría a alcanzar la altura inicial desde la que fue lanzado.
a) El movimiento sobre un plano horizontal, una vez comenzado, debería ser permanente, de acuerdo a los razonamientos de Galileo.
b) En la práctica esto pudiera lograrse eliminando totalmente las fuerzas de rozamiento o fricción entre el cuerpo y la superficie, lo que es una situación ideal. Se puede disminuir el rozamiento pero no anularlo.
: Experimento con una esfera suspendida de una cuerda a un soporte fijo
Te invitamos a probar la realización del siguiente experimento:
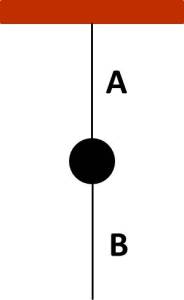
Tomas una esfera (o cuerpo) de 1,0 kg, aproximadamente, la suspendes de un soporte mediante una cuerda, y una segunda cuerda del mismo material la fijas en la parte inferior del cuerpo, de manera que el conjunto quede de acuerdo a la figura que se muestra.
a) Si tiras violentamente de la cuerda B, ¿qué ocurre ?
b) Si se tira de la cuerda B no violentamente, sino en forma continua, aumentando cada vez con una fuerza más grande, se rompe la cuerda A.
Explica la causa de que en un caso se rompa la cuerda de la parte inferior (B) y en el otro se rompa la cuerda de la parte superior (A).
: Tercera ley del movimiento
Si las fuerzas de acción y reacción son de igual valor o módulo, actúan en la misma dirección y son de sentido contrario, ¿por qué no se equilibran?
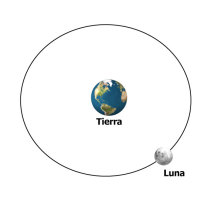
La Tierra y nuestro satélite natural, la Luna
Análisis, solución y respuesta:
Si analizamos la interacción entre dos cuerpos cualesquiera en el Universo, por ejemplo, la interacción entre la Tierra y la Luna, dicha interacción cumple, como, se conoce con la tercera ley del movimiento enunciada por Newton: la fuerza que le ejerce la Tierra a la Luna y la que le ejerce la Luna a la Tierra, son iguales en valor modular, actúan en la misma dirección pero son de sentido contrario. No pueden anularse porque actúan sobre cuerpos diferentes, una de ellas actúa sobre la Luna y la otra actúa sobre la Tierra (ver figura).
Fuerzas de interacción entre la Tierra y la Luna
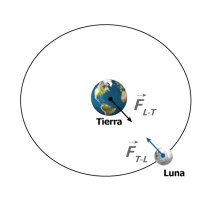
Para que dos fuerzas de igual valor o módulo, de la misma dirección y de sentido contrario se equilibren, es decir, se anulen sus efectos, estas dos fuerzas deben estar actuando sobre el mismo cuerpo, tener el mismo punto de aplicación.
Bloque que se lanza sobre la superficie de una mesa horizontal
La fuerza de gravedad y la fuerza normal que actúan sobre un bloque que se lanza sobre la superficie horizontal de una mesa se equilibran, anulan sus efectos. La fuerza que causa que el bloque disminuya el valor de la velocidad hasta detenerse el la fuerza de rozamiento entre el bloque y la superficie de la mesa.
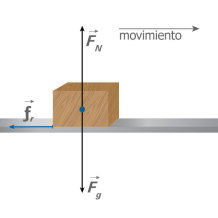
: Aplicaciones de la segunda ley del movimiento: Cálculo de la fuerza de fricción que actúa sobre un bloque
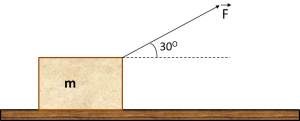
Sobre una superficie horizontal se encuentra en reposo un bloque de 10 kg. Si sobre este actúa una fuerza de 60 N que forma un ángulo de 30º con la horizontal, como se muestra en la figura, y el coeficiente de fricción cinético entre el bloque y la superficie es 0,30. Calcula el valor de la fuerza de fricción que actúa sobre el cuerpo.
: Aplicaciones de la segunda ley del movimiento: Fuerza necesaria para bajar un cuerpo por un plano inclinado con velocidad constante
Por un plano inclinado de 2,4 m de longitud y 1,2 m de altura hay que bajar un cuerpo (bloque) de 2,5 kg con velocidad constante. Si el coeficiente de rozamiento entre el cuerpo y la superficie del plano es 0,4.
a) ¿Será preciso empujar el cuerpo hacia abajo o tirar de él hacia arriba? Argumenta tu respuesta.
b) ¿Qué fuerza paralela al plano es necesaria para obtener el movimiento con velocidad constante?
: Aplicaciones de la segunda ley del movimiento: Fuerza resultante que actúa sobre un vehículo
El valor de la velocidad de un vehículo de 520 kg de masa que se mueve por una carretera recta, aumenta uniformemente de 4 m/s a 12 m/s en 4 s.
¿Qué valor tiene la fuerza neta que actúa sobre él?
Análisis del problema:
Como debe determinarse el valor de la fuerza neta sobre el vehículo se debe aplicar la segunda ley del movimiento:
Ell movimiento se realiza en una dirección se puede utilizar la ecuación de la segunda ley del movimiento:
(1)
Se conoce por dato la masa del vehículo y no el valor de la aceleración del movimiento, este dato se puede determinar por la ecuación cinemática de la aceleración:
(2)
Solución y respuesta:
Para calcular la fuerza neta o resultante se sustituye (2) en (1):
Esta es la ecuación solución que da respuesta al problema.
Sustituyendo por datos y resolviendo las operaciones queda:
La fuerza neta sobre el vehículo es de 1 040 N.
: Aplicaciones de la segunda ley del movimiento: Velocidad que llevaba un tren que se detiene por la acción de la fuerza de rozamiento
Un tren que pesa 4,9 · 106N, una vez que la máquina interrumpe la tracción, se detiene al cabo de 1 minuto por la acción de la fuerza de rozamiento, que es igual a 9,8 · 104 N. ¿A qué velocidad marchaba el tren?
: Aplicaciones de la segunda ley del movimiento: Diseño de un globo para investigaciones atmosféricas
Se necesita diseñar un globo para investigaciones atmosféricas que pueda alcanzar, partiendo del reposo una altura de 1,0 · 103 m en 10 s. Considere que, además de la fuerza de gravedad, sobre el globo actúa una fuerza de empuje constante de 1 000 N en dirección vertical y hacia arriba.
a) Calcula la aceleración con que ascenderá el globo.
b) Determina la masa del globo.
c) Si en otras condiciones se necesita que el globo ascienda con movimiento rectilíneo uniforme, ¿en cuánto se debe aumentar la masa del globo para lograr esto?
Considera g = 9,8 m/s2