Se necesita diseñar un globo para investigaciones atmosféricas que pueda alcanzar, partiendo del reposo una altura de 1,0 · 10³ m en 10 s. Considere que, además de la fuerza de gravedad, sobre el globo actúa una fuerza de empuje constante de 1 000 N en dirección vertical y hacia arriba.

a) Calcula la aceleración con que ascenderá el globo.

b) Determina la masa del globo.

c) Si en otras condiciones se necesita que el globo ascienda con movimiento rectilíneo uniforme, ¿en cuánto se debe aumentar la masa del globo para lograr esto?

Considera g = 10 m/s²

Análisis del problema, resolución y respuesta:

Sobre el globo que asciende, actúan dos fuerzas constantes: la fuerza de gravedad y la fuerza de empuje, por lo que la resultante de estas hace que el globo ascienda con aceleración constante.

Para resolver este problema se debe aplicar la segunda ley del movimiento de Newton:

$\overrightarrow{F_{\mathit{res}}}=m\vec{a}$

Las incógnitas que plantea el problema son:

a) a - ¿?

b) m - ¿?

c) Δm - ¿? para que el globo ascienda con M.R.U.

¿Qué datos se conocen?

v₀ = 0

y = 1,0 · 10³m

Δt = 10 s

F_e= 1 000 N

Para calcular la aceleración con que asciende el globo se hace uso de la ecuación cinemática del M.R.U.A. :

$y=v_{0}t+\frac{1}{2}{\mathit{at}}^2$

Como v₀ = 0

$\begin{array}{c}y=\frac{1}{2}{a}_y{t}^2\\ a_y=\frac{2y}{t^2}\end{array}$

Sustituyendo por datos y resolviendo la operación queda:

$\begin{array}{c}a=\frac{2(1·{10}^{3}m)}{100s^2}\\ a=20\frac{m}{s^2}\end{array}$

La aceleración con que asciende el globo es de 20 m/s².

b) Para determinar la masa del globo que asciende con aceleración se analizan las fuerzas que actúan sobre este:

Se aplica la ecuación de la segunda ley del movimiento de Newton:

$\overrightarrow{F_{\mathit{res}}}=m\vec{a}$

$\overrightarrow{F_e}-\overrightarrow{F_g}=m\overrightarrow{a_y}$

Se adopta el sentido del movimiento como positivo:

$\begin{array}{c}{F}_e-F_g=m{a}_y\\ F_e=F_g+m{a}_y\end{array}$

Como:

$\begin{array}{c}{F}_g=\mathit{mg}\\ F_e=\mathit{mg}+m{a}_y\end{array}$

$\begin{array}{c}{F}_e=m(g+a_y)\\ m=\frac{F_e}{g+a_y}\end{array}$

Sustituyendo por datos y calculando queda:

$\begin{array}{c}m=\frac{1·{10}^{3}N}{(\mathrm{9,8}+20)\frac{m}{s^2}}\\ m\approx \mathrm{33,6}\mathit{kg}\end{array}$

La masa del globo es de aproximadamente 33,6 kg.

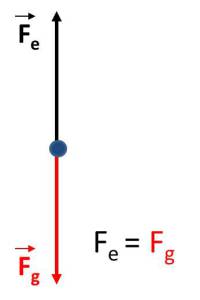
c) Se deben analizar las características de las fuerzas que actúan sobre el globo para que ascienda con M.R.U.:

Al aplicar la segunda ley de Newton para este caso queda:

$\begin{array}{c}{F}_e-F_g=0\\ F_e=m_{0}g\end{array}$

se despeja la masa que debe tener el globo para ascender con M.R.U., se sustituye por datos y se resuelve la operación:

$\begin{array}{c}{m}_0=\frac{F_e}{g}\\ m_0=\frac{1·{10}^{3}N}{\mathrm{9,8}\frac{m}{s^2}}\end{array}$

$m_0\approx 102\mathit{kg}$

Como la incógnita planteada es el aumento de la masa del globo para que ascienda con movimiento rectilíneo y uniforme, se tiene que:

$\begin{array}{c}\mathrm{\Delta }m=m-m_0\\ \mathrm{\Delta }m=102\mathit{kg}-\mathrm{33,6}\mathit{kg}\end{array}$

$\mathrm{\Delta }m=\mathrm{68,4}\mathit{kg}$

La masa del globo debe aumentarse en 68,4 kg, aproximadamente para que este ascienda con M.R.U.