Ecuación del movimiento ondulatorio
Fundamental : ¿Cómo determinar la coordenada de cada punto por el que se propaga una onda en función del tiempo?
Supongamos que el punto en el cual se producen las oscilaciones armónicas que se propagan unidireccionalmente oscila en correspondencia con la ecuación:
y = A sen (ωt)
donde y es la A, la ω es la frecuencia angular y t es el tiempo.

La oscilación se propaga a todos los puntos del medio con cierto retraso fase respecto al foco. Si la onda llega al punto P situado a una distancia x al cabo de un intervalo Δt, y suponemos que las oscilaciones no amortiguan, la elongación de dicho punto en función del tiempo vendrá dada por la ecuación:
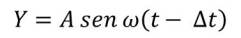
donde la velocidad de propagación es constante e igual a v
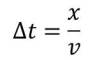
la ecuación toma la forma:
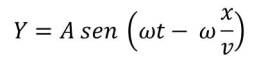
Si tomamos, además, en consideración que:
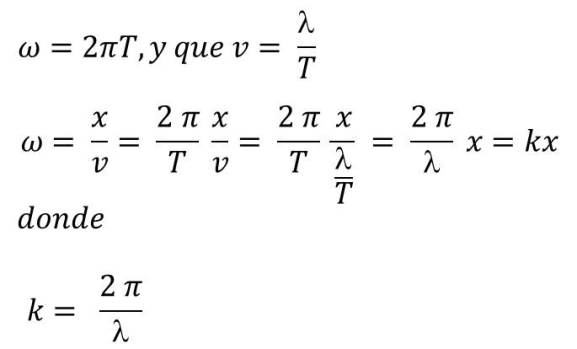
La constante k es análoga a ω, pero en sentido espacial, k es el número de λ en 2π rad.
En términos de los parámetros ω y k la ecuación adopta la forma:
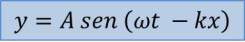
Análisis gráfico de la ecuación
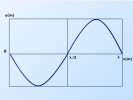
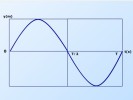
Como y es función de t y de x, esta ecuación está caracterizada por dos gráficas: y= f(t) para cada valor de x y y=f(x) para cada valor de tiempo (t)
Representa la configuración de la onda en un instante determinado de tiempo, o sea, es la gráfica de la ecuación de la elongación en función de la coordenada de cada punto para un instante de tiempo determinado. | Representa cómo varía en función del tiempo la elongación de un punto de coordenada x, es decir, es la gráfica de la ecuación del movimiento de cada uno de los puntos de la región por la cual se propaga la onda. |