Péndulo simple

Construye un péndulo simple y determina:
el período de oscilación
la frecuencia
El péndulo simple es un modelo matemático, pues puede considerarse como un sistema formado por un hilo inextensible, cuya masa se considera despreciable, un cuerpo considerado puntual que cuelga del hilo y la Tierra. En realidad un péndulo construido cuidadosamente por ti se comportará muy aproximadamente como si fuera ideal. Esto lo puedes comprobar en la práctica si, por ejemplo quieres determinar el período de tu péndulo, haciendo las mediciones correspondientes y comparando el valor hallado con el calculado mediante las ecuaciones.
Para facilitar el análisis se toman desviaciones muy pequeñas de la posición de equilibrio, o sea, pequeñas amplitudes, (ө --> 0), donde la trayectoria del cuerpo puede considerarse un segmento de línea recta. Entonces puede asumirse con bastante aproximación que la fuerza de la gravedad que actúa sobre él tiene un valor:
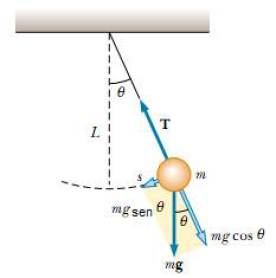
F = -mg sen ө (25)
De trigonometría conocemos que cuando θ ≈ 0 entonces:
sen ө ≈ ө (26)
Estando el valor de ө expresado en radianes. Puede plantearse con una buena aproximación:
F = -m g ө (27)
Como:
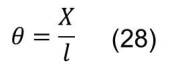
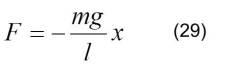
De aquí se deduce que, de acuerdo a la ecuación (13):
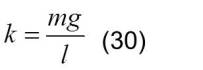
Como el período es:
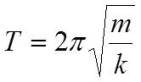
Sustituyendo k:
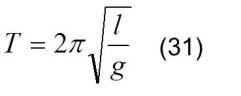
La frecuencia:
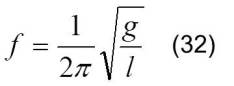
Por lo tanto, para oscilaciones de pequeña amplitud el período y la frecuencia dependen solo de la longitud (l) y de la aceleración de la gravedad (g).