Dinámica del MAS
Analicemos el carácter de la fuerza bajo la cual se producen las oscilaciones armónicas.
SISTEMA CUERPO RESORTE
Al oscilar un sistema cuerpo-resorte describe en el papel que se mueve la curva de una función armónica.
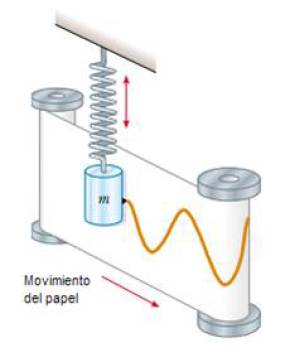
Utilizando las ecuaciones llegaremos a otras relaciones, también importantes, que brindan más información sobre las características del movimiento oscilatorio mecánico y que son de utilidad para el estudio de otros movimientos, como el ondulatorio.
En el MAS se ponen de manifiesto dos elementos contradictorios: una fuerza recuperadora y un elemento inercial.
La fuerza recuperadora es aquella que hace que el cuerpo retorne a la posición de equilibrio una vez que alcance la amplitud de su movimiento.
Supongamos que la fuerza recuperadora tiene la forma:
F = - kx (1)
donde k es la constante elástica.
Una fuerza de este tipo puede proporcionarla un cuerpo elástico, tal como una banda de goma o un resorte. La magnitud x representa la elongación, por lo que se evidencia que en el punto de equilibrio (x = 0) la fuerza recuperadora es nula. El signo menos indica que el sentido de la fuerza es siempre contrario al sentido de aumento de la elongación.
El elemento inercial hace que el cuerpo, una vez que arriba a la posición de equilibrio, continúe su movimiento hasta llegar a la máxima elongación (en sentido opuesto), para repetir el ciclo.
En el caso particular del MAS mecánico el elemento inercial es la masa.
Por la segunda ley de Newton:
F = ma (2)
Igualando (1) y (2):
- k x = ma (3)
Para el análisis del MAS consideramos que:
· No existen fuerzas disipativas (fricción), por lo que la energía mecánica se conserva.
· No existe agente externo actuando sobre el sistema, salvo en el momento de excitación inicial.
Anteriormente vimos que:
x = A sen (ωt + φ) (4)
a = - w2A sen (ωt + φ) (5)
Sustituyendo (4) y (5) en (3) y simplificando se obtiene: k = m ω2 (6)
O sea, bajo los efectos de una fuerza del tipo (1), un cuerpo de dimensiones puntuales realizará un MAS, si se cumple la condición (6).
De (6) se deduce que la frecuencia angular:
Lo que significa que esta magnitud únicamente depende de la masa m y de la constante elástica k.
Completaremos el estudio de la dinámica del MAS realizando un análisis energético del mismo.
La energía cinética:
La energía potencial elástica:
Como se ha dicho, en el MAS no hay agentes disipativos, por lo que la energía mecánica se conserva. Un análisis desde el punto de vista energético muestra que en los puntos de máxima elongación, el sistema no posee energía cinética (instantáneamente está en reposo) y por tanto toda su energía es potencial. Por el contrario, al pasar por la posición de equilibrio, la energía potencial es mínima y máxima la cinética. En cada punto del movimiento, la suma de ambas energías (cinética y potencial) da un valor constante, que es la energía mecánica total.