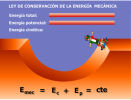
Ley de conservación de la energía mecánica
Estudio de caso : La Física de la montaña rusa
En las ferias y espectáculos uno de los números más llamativos está relacionado con el giro de la muerte, en el que uno o varios móviles dan una vuelta completa en el plano vertical.
Esta situación se presenta en algunos tipos de montaña rusa y con motos o bicicletas que se lanzan desde una rampa hasta llegar al rizo.
¿Qué relación tiene la energía con lograr la vuelta completa?
Para dar respuesta a la interrogante, determina la altura mínima que debe tener una rampa, para que una bicicleta u otro móvil que se deja caer por ella realice una vuelta completa. Analiza que condiciones debe cumplir la energía en esta situación.
Para lograr una vuelta exitosa en el rizo, es necesario tener en cuenta la altura inicial, el diámetro del rizo y la velocidad en el punto más alto de la trayectoria, entre otros factores.
Durante el movimiento del cuerpo en la montaña rusa la energía inicial puesta en en juego, se transforma de un tipo en otro, pero finalmente se conserva.
Explicación energética de un patinador por una rampa
|
|
|
Al analizar las ilustraciones del patinador podemos destacar que:
En el punto más bajo de la rampa, la energía potencial del patinador es igual a cero.
En cualquier punto de la trayectoria, la suma de las energías cinética y potencial del patinado es igual a la energía mecánica.
La velocidad del patinador es mayor en el punto de altura mínima y por tanto su energía cinética es máxima.
Si en un sistema aislado solo actúan fuerzas conservativas[1], por ejemplo, la fuerza de gravedad o la fuerza elástica, la energía mecánica del sistema se conserva. Esto significa que la energía mecánica inicial es igual a la energía mecánica final.
Entendemos a la energía mecánica como la energía asociada al movimiento y las interacciones de un cuerpo como un todo.
: Ley de conservación de la energía mecánica
La suma de las energías cinética y potencial de los cuerpos que están en interacción por medio de fuerzas conservativas, permanece siempre constante.
: Problema resuelto 1
Un auto parte del reposo desde lo alto de una superficie inclinada, como se representa en la figura. Determina el valor de la velocidad del auto al llegar a la superficie horizontal.
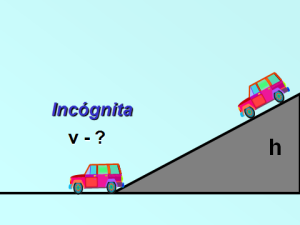
Análisis y solución
A partir de la ley de conservación de la energía mecánica encontraremos la ecuación que nos permite resolver el problema:
Determinada la ecuación se sustituyen por los valores de las magnitudes involucradas y obtendremos el valor deseado. En este caso el propósito es llegar a la ecuación que permite hacer ese cálculo.
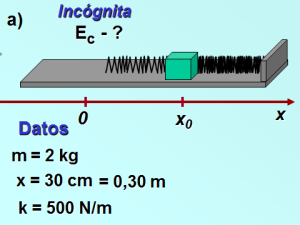
: Problema resuelto 2
Un bloque de 2 Kg de masa comprime 30 cm un resorte, de constante elástica igual a 500 N/m, hasta detenerse.
a) Determina la energía cinética del sistema al pasar por la posición de equilibrio.
b) Determina el valor de la velocidad al pasar por la posición de equilibrio.
Análisis y solución
A partir de la ley de conservación de la energía mecánica encontraremos la ecuación que nos permite resolver el problema, luego sustituimos con los datos que se ofrecen:
inciso a)
inciso b)
Siguiendo el enlace encontrarás otros ejercicios resueltos donde se aplica la ley de conservación y transformación de la energía mecánica.
