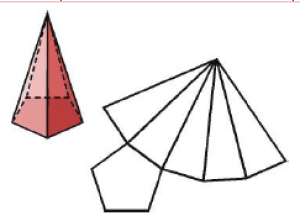
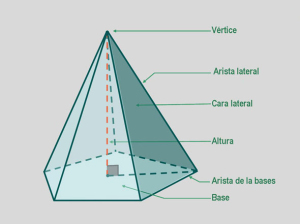
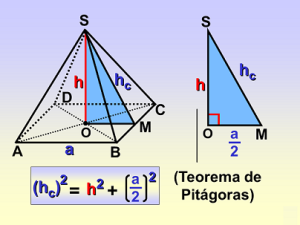
Pirámides. Áreas y volúmnes

Las pirámides son uno de los cuerpos geométricos más conocidos y de fácil identificación, quién no ha oído hablar y has visto imágenes de las famosas pirámides de Egipto, de las pirámides mayas , la Torre del Louvre entre otras. Todas ellas se caracterizan por su forma y de las cuales existen leyendas interesantes.

De la pirámide como cuerpo geométrico estudiaste su definición y elementos.

¿ Qué diferencia a las pirámides de otros cuerpos geométricos?

¿Cómo calcular el área y el volumen e una pirámide conocido un angulo y una arista?

Recuerda que...

Todo cuerpo limitado por una superficie poligonal y n superficies triangulares congruentes en un punto se llama pirámide de n lados .

Fundamental

Es importante saber diferenciar los elementos que caracterizan a las pirámides

Como sus caras son triangulares, cada una de sus caras posee una altura que no es igual a la altura del cuerpo ni a la longitud de la arista lateral,donde en ocasiones es necesario aplicar el teorema de Pitágoras para calcular alguno de sus elementos o las razones trigonométricas, para poder conocer otros elementos por lo que en necesario saber diferenciarlos.

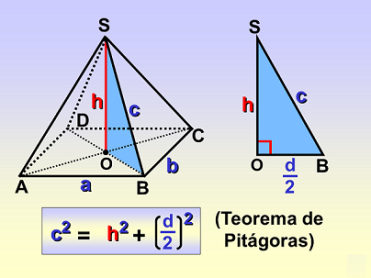
Para recordar ...¿Cómo se determina el volumen de una pirámide?

Debes recordar que el volumen de la pirámide guarda relación con el volumen de un prisma de igual base y altura , es decir, el volumen de una pirámide es la tercera parte del volumen de un prisma de igual área de la base y altura , matemáticamente se expresa a través de la fórmula, V = A B ⋅ h 3 V= { A_{B} cdot h } over {3}

Puedes observar un ejemplo en un prisma de base triangular.

Al igual que en los prismas , solo trabajarás con pirámides rectas,. Dentro de estas  vas a encontrar las pirámides llamadas pirámides regulares.

¿ Cómo determinar el área y/o el volumen de una pirámide cuando se conoce solamente la longitud de la altura de una cara o arista y el ángulo que esta forma con la base?

EjemploEjemplo 3

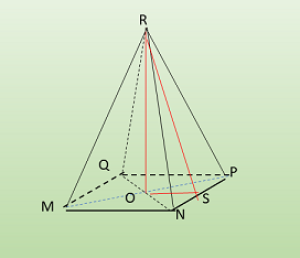
De una pirámide regular se conoce que:

A B = 3600 cm 2 A_{B}= 3600 cm^{2}

S S es punto medio de PN ˉ bar PN , ∢ ORS = 30 0 %angle ORS = 30^{0}

RO ˉ bar RO es la altura de la pirámide.

¿ Cuál es el valor de su área lateral y de su volumen?

Ver solución [pdf]