La función cuadrática y sus propiedades
Meditar :
Todas estas situaciones describen trayectorias parabólicas que siguen modelos de funciones cuadráticas.
Las funciones cuadráticas han servido para construir modelos matemáticos que explican ciertos comportamientos en las áreas de Ciencias Naturales , Física así como en numerosos estudios científicos.
Saber más :
Un grupo de investigadores realizaron una experiencia sobre los efectos nutricionales en ratas, con una dieta que contenía un 10 % de proteína. Esta consistió en levadura y harina de maíz. Variando el porcentaje p de levadura en la mezcla de proteína se estimó que el promedio ganado (en gramos) de una rata en un periodo de 100 días f (p) , se obtiene a través de una función cuadrática dada por la ecuación:
Propiedades de una función cuadrática
Al analizar una función cuadrática cualesquiera debes tener en cuenta la influencia de los parámetros en la gráfica y en algunas de sus propiedades.
Por ejemplo en una una función cuadrática definida por una ecuación de la forma
El dominio de definición es el conjunto de los números reales, aunque en ocasiones se indica una restricción de este, es necesaria la restricción atendiendo a la problemática que se modela.
El conjunto imagen, la abertura y la existencia de máximo o mínimo dependen de la ordenada del vértice y de la condición que cumple el parámetro a.
Si la parábola abre hacia arriba, el conjunto imagen esy tiene como valor mínimo la ordenada del vértice .
Si la parábola abre hacia abajo el conjunto imagen es y tiene como valor máximo la ordenada del vértice .
Las coordenadas del vértice son , donde .
Esta curva es simétrica y el eje de simetría esque es una recta paralela al eje de las ordenadas.
La función es par si se cumple que .
La monotonía de la función cuadrática depende de la abscisa del vértice y de la condición que cumple el parámetro a.
Si , la función es creciente para y decreciente para
Si , la función es creciente para y decreciente para
Los ceros de la función son los valores del dominio para los cuales se cumple . Gráficamente los ceros de la función son los puntos de corte de la parábola con el eje de las abscisas.
Ejemplo :
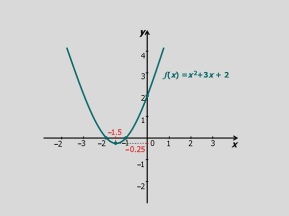
De la parábola que aparece a continuación, identifica:
Su conjunto dominio
El conjunto imagen
Ceros de la función
Investiga si la función es par
Escribe un intervalo donde la función sea creciente y negativa.
La función cuadrática también puede ser expresada a través de una ecuación donde las coordenadas del vértice son. Esta forma facilita el análisis de las propiedades de la función trasladada -d unidades en dirección del eje de las abscisas y e unidades en dirección al eje de las ordenadas de la parábola normal[1] de ecuación .
En particular la existencia de ceros depende del valor de e
Si entonces la función tiene dos ceros[2] por lo que su gráfica intersecta al eje de las abscisas en dos puntos.
Si la función tiene un solo cero[3], gráficamente la parábola solo corta al eje de las x en un punto.
Si la función no tiene ceros[4] , la interpretación gráfica la parabola se encuentra por encima del eje x.
Ejemplo :
La ecuación corresponde a una función cuadrática, de esta analiza :
a) ¿Cuáles son las coordenadas del vértice?
b) ¿Cuál es el conjunto imagen de la función?
c) ¿Para qué valores del dominio las función es creciente?
d) ¿Cuál es el menor valor que puede tomar la función?
