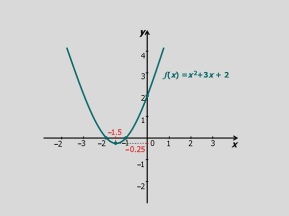
SOLUCIÓN

• La variable independiente puede tomar cualquier valor real por lo que su conjunto dominio es$R$

• Las coordenadas del vértice son(-1,5;-0,25) por lo que el valor minimizo es -0,25 esto significa que el conjunto imagen son todos reales , tales que $y\ge -\mathrm{0,25}$

• Para hallar los ceros observamos los puntos de corte de la parábola con el eje de las abscisas. Por lo que los ceros son x=-2 y x=-1

• Para determinar analíticamente si la función es par se debe evaluar la función para un valor del dominio y su opuesto y comprobar que sus imágenes son iguales$f\left(x\right)=f\left(-x\right)$.

  Por ejemplo $f\left(1\right)=6$ y $f\left(-1\right)=0$por eso no es una función par.