La función lineal y sus propiedades

Meditar :
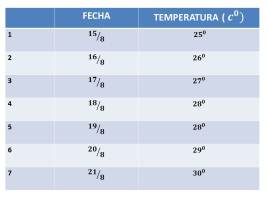
Un meteorólogo registró durante varios días la temperatura, como se refleja en la tabla
¿Cómo puedes representar la relación entre los días y sus respectivas temperaturas?
¿Es posible graficar este comportamiento?
¿Cuál es el modelo que relaciona estas magnitudes?
La función lineal
En particular, una función lineal se expresa analíticamente a través de una ecuación de la forma f(x) = m x + n y gráficamente por una recta que expresa las relaciones entre las variables y entre los parámetros[1] .
Generalmente la variable independiente se identifica por la letra x mientras que la variable dependiente por la letra y.
Atención :
Cuando se trata de procesos, deben emplearse las variables correspondientes a las magnitudes que se relacionan en la función para analizar su comportamiento. Así por ejemplo cuando se desea analizar el comportamiento de la temperatura de un lugar atendiendo a la altura, la variable independiente h corresponde a la altura y la dependiente T a la temperatura, por lo que la función puede ser expresada a través de la ecuación . En este caso m y n son parámetros.
Propiedades de las funciones lineales
Al analizar una función podemos determinar:
el conjunto dominio y el conjunto imagen
la monotonía
los ceros
el signo de la función
la paridad.
estas pueden ser analizadas en cualquiera de las formas en que pueden ser expresadas las funciones.
Con estas propiedades podemos dar respuesta a situaciones que puedan modelarse a partir de una función lineal.
Ejemplo :
En el sistema de coordenadas se ha representado el comportamiento de una llamada telefónica que se realizó desde un teléfono fijo en horario diurno.
a) ¿Cuál es la ecuación que permite conocer el gasto por llamada según el tiempo de duración de esta?
b) ¿Cuánto hubiera costado la llamada, si hubiera hablado solo 10 minutos?
c) Si el importe de la llamada fue de $2,70, ¿qué tiempo estuvo hablando el usuario?
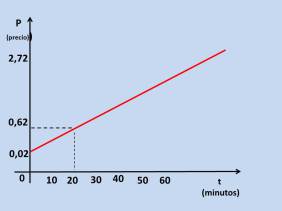
Las funciones lineales pueden ser representadas gráficamente, siendo suficiente determinar dos pares ordenados que correspondan a la función. Las gráficas ofrecen una mayor visión sobre la trayectoria o comportamiento del proceso que se estudia.
¿Sabías que...? :
El economista, matemático y obispo Nicole de Oresme (1323-1382) fue quien realizó la innovación de la representación gráfica de una función, trazó gráficas de las variaciones de la velocidad, la temperatura, la intensidad luminosa y otros fenómenos de diversa índole. Utilizaba las expresiones de "longitud" y "latitud", netamente para la representación de las trayectorias de los astros, llevándolo a la representación gráfica.
