Ejercicios resueltos
: Aplicación de la ley de Gravitación Universal
Calcula la fuerza de Gravitación Universal entre la Tierra y la Luna y representa estas fuerzas en un diagrama.
Considera que la distancia desde el centro de la Tierra hasta la Luna es de .
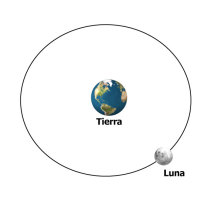
La Luna, nuestro satélite natural, orbita alrededor de la Tierra en un período de días.
Análisis, solución y respuesta:
La fuerza de gravitación universal entre dos cuerpos cualesquiera es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa, de acuerdo a la expresión:
Sustituyendo por los datos y resolviendo las operaciones planteadas, queda:
Sustituyendo por los datos y resolviendo las operaciones, queda:
La fuerza de gravitación entre la Tierra y la Luna es de 3,3 · 1024 N.

Fuerzas de interacción gravitatoria entre la Tierra y la Luna
Estas fuerzas cumplen con la tercera ley de Newton, son un par de fuerzas de acción y reacción.
: Cálculo de la masa del Sol
Determina la masa del Sol.