Ley de gravitación universal
Desde que adquirimos noción del mundo, asumimos como algo natural el movimiento del Sol en el cielo, más tarde nos explican en la escuela que la Tierra se traslada alrededor del Sol y que está separada de él a la distancia media aproximada de 150 millones de kilómetros y ahí es cuando nos preguntamos, ¿por qué la Tierra gira alrededor del Sol?, ¿cuál es la relación entre la distancia que los separa y sus masas?
Estudio de caso :
Los primeros esfuerzos de Newton en comprender el movimiento de los cuerpos celestes los dirigió hacia la Luna. Por sus conocimientos acerca del movimiento de los cuerpos en la Tierra sabía que si la Luna no se movía en línea recta y con velocidad constante era porque sobre ella se ejercía una fuerza que era la causa de que el satélite curvara su trayectoria. ¿Cuál es la fuerza que hace que la Luna se mueva alrededor de la Tierra?
Cuentan que Newton dijo que la respuesta a esta interrogante la encontró un día que meditaba sentado en el jardín y una manzana cayó al suelo; entonces pensó, que la fuerza que la Tierra ejercía sobre la manzana, también podía ejercerse sobre la Luna. ¿Serán correctas las suposiciones de este eminente científico?

: Ley de gravitación universal

Todos los cuerpos en el Universo, se atraen con una fuerza que es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que separa sus centros.
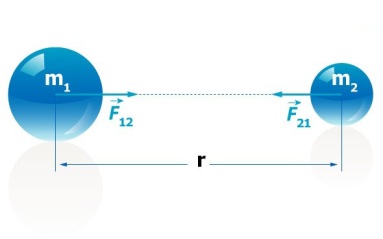
La interacción gravitatoria ocurre entre cuerpos que poseen masa y es siempre de atracción.
El valor de esa fuerza puede ser calculada según la expresión:
Donde G es la constante de gravitación universal y su valor es:
Sobre la acción gravitatoria
La acción gravitatoria es independiente de la naturaleza de los cuerpos, solo depende de sus masas y la distancia entre ellos.
Las fuerzas de gravitación actúan en pares de acción y reacción.
La intensidad de la fuerza gravitacional varía proporcionalmente con la masa de los cuerpos. Para cuerpos de grandes masa esta fuerza es significativa, por ejemplo, entre el Sol y la Tierra, entre la Tierra y la Luna, en las interacciones entre galaxias y estrellas. En la superficie de la Tierra, la atracción gravitacional entre los cuerpos no es percibida, porque las masas son muy pequeñas si se comparan con la de los cuerpos celestes, por tal razón la noción de gravedad es asociada solamente a la Tierra y no a los cuerpos que en ella se encuentran. Para distancias pequeñas la fuerza aumenta, pero a distancias atómicas prevalecen otras fuerzas.entre otros.
: Campo gravitatorio
La interacción entre dos cuerpos de masa m y M se realiza a través del campo gravitatorio.
El campo gravitatorio es un tipo de materia que se manifiesta por la acción que ejerce este sobre los cuerpos.
El campo gravitatorio es un tipo de materia que se manifiesta por la acción que ejerce este sobre los cuerpos.
¿De qué factores dependen las acciones del campo gravitatorio de un cuerpo en un punto determinado?
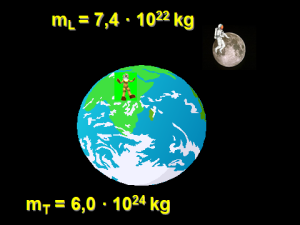
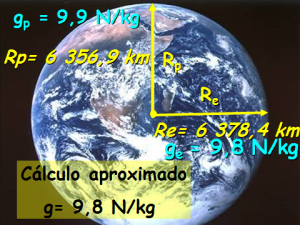
Uno de los factores que es la masa del cuerpo, así, el valor de "g" en la Tierra es mayor que en la Luna.
El otro factor que incide sobre la intensidad del campo gravitatorio es la distancia del cuerpo al punto. Por ejemplo: la intensidad del campo gravitatorio "g" en los polos de la Tierra es mayor que la del ecuador, sin embargo, la distancia del centro de la Tierra a los polos, es menor que la que existe hasta el ecuador terrestre.
Estas magnitudes se relacionan de modo que:
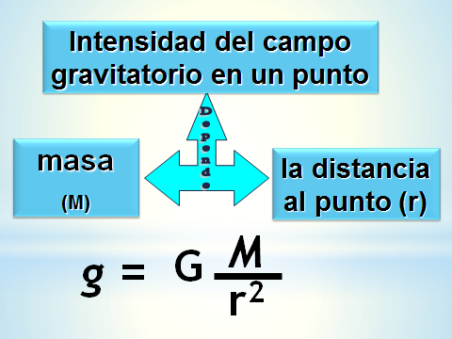
Saber más : Intensidad del campo gravitatorio de los planetas del Sistema Solar
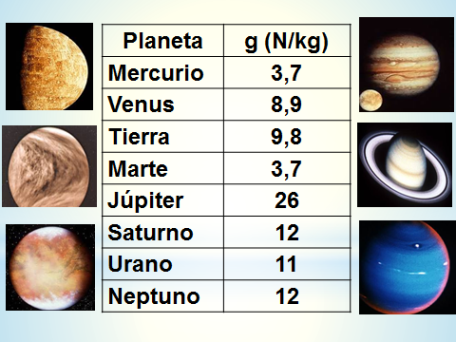
: Problema resuelto

Determina el módulo de la fuerza entre la Tierra y el Sol.
Saber más :
Comprobación experimental de la ley de gravitación universal
La balanza de torsión ideada por Cavendish para demostrar experimentalmente la existencia de la interacción gravitatoria le permitió calcular el valor de la constante de gravitación universal que lleva su nombre. Cavendish utilizó un rayo de luz y un espejo para detectar la más mínima torsión producto de la interacción.
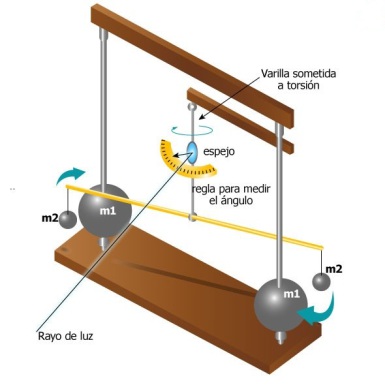
La balanza de torsión ideada por Cavendish para demostrar experimentalmente la existencia de la interacción gravitatoria le permitió calcular el valor de la constante de gravitación universal que lleva su nombre. Cavendish utilizó un rayo de luz y un espejo para detectar la más mínima torsión producto de la interacción.
Algo de historia : De Kepler a Cavendish
Johannes Kepler, a finales del siglo XVI y principios del XVII, obtuvo experimentalmente (mediante la observación) las leyes cinemáticas que describen el movimiento de los planetas. El fundamento teórico de estas leyes, conocidas como leyes de Kepler, fue explicado años después, por Isaac Newton al enunciar una de las leyes fundamentales del universo, la ley de gravitación universal. El valor de la constante de gravitación universal fue hallado experimentalmente en 1790 por el Henry Cavendish utilizando una balanza de torsión.
Saber más : La constante de Cavendish
El valor numérico de la constante de Cavendish es sumamente pequeño:
Para lograr una fuerza de interacción de 9,8 N, que es la fuerza con que la Tierra atrae hacia su centro a un cuerpo de 1 kg, es necesario que el producto de las masas de los cuerpos que interactúan, separados a una distancia de 1m, sea igual a: 1.46 x 108 kg2, inmensa.
La fuerza de interacción gravitatoria entre dos personas, separadas a la distancia de un metro, cuya masa es de 80 kg es solo de: 4,28 x 10-4 N, imperceptible.
Esa es la razón por la cual no notamos la interacción gravitatoria entre los cuerpos cotidianamente. Únicamente con la Tierra es apreciable, debido a su masa inmensa.

¿Sabías que...? : Predicción de un nuevo planeta
Newton aplicó la ley de gravitación universal a una gran variedad de problemas. Entre otros analizó también las pequeñas irregularidades de las órbitas planetarias. Posteriormente, esta teoría de perturbaciones condujo al descubrimiento de un nuevo planeta.
Saber más :
La velocidad V0= 8 km/s se denomina primera velocidad cósmica. Cualquier cuerpo lanzado con esta velocidad desde la Tierra describe una trayectoria circular alrededor de la misma convirtiéndose en satélite artificial.
La velocidad V0= 11,2 km/s se nombra segunda velocidad cósmica ó velocidad parabólica. Los cuerpos lanzados con velocidades iguales o mayores a ésta, se alejarán del planeta Tierra siguiendo una trayectoria parabólica o hiperbólica.
Para velocidades menores que 8 km/s el cuerpo caerá de nuevo en la Tierra y para mayores que esta pero menores que 11.2 km/s se convertirá en un satélite artificial. Para velocidades mayores que 11.2 km/s el cuerpo se alejará definitivamente de la Tierra.