La llamada telefónica
Ejemplo :
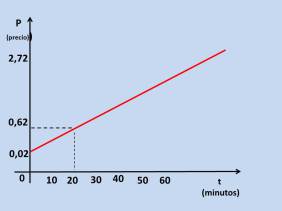
En el sistema de coordenadas se ha representado el comportamiento de una llamada telefónica que se realizó desde un teléfono fijo en horario diurno .
a) ¿Cuál es la ecuación que permite conocer el gasto por llamada según el tiempo de duración de esta?
b) ¿Cuánto hubiera costado la llamada, si hubiera hablado solo 10 minutos?
c) Si el importe de la llamada fue de $2,70, ¿qué tiempo estuvo hablando el usuario?
a) Para determinar la ecuación que relaciona el precio a pagar por la llamada en función del tiempo de duración de esta, debemos declarar primeramente las variables que utilizarás:
Si consideras P el precio y t el tiempo de duración de la llamada, la ecuación puede escribirse P(t) = mt + n
El intersecto de la recta con el eje y indica el valor del parámetro n, en este caso 0,02,
Para determinar la pendiente basta sustituir en la ecuación P(t) = mt + n, las coordenadas de un punto del cual podamos leer sus coordenadas en el gráfico (20 ; 0,62) y despejamos m
P(t) = mt + n
0,62 = m(20) + 0,02
0,60 = m(20)
m =0,60 :20
m = 0,03 y significa que cada minuto tiene un valor de $ 0.03
por lo que la ecuación es: P(t) = 0,03t + 0.02
b) Como ya conoces la ecuación que modela el precio de la llamada en función del tiempo de duración, para determinar el costo de la llamada al conversar 10 minutos sustituimos el tiempo y calculas.:
P(t) = 0,03t + 0.02
= 0,03 (10)+ 0.02
= 0,3 + 0.02
= 0,32
El costo de la llamada es de 32 centavos.
c) Análogamente al procedimiento seguido en el inciso anterior sustituyes el valor pagado $2,72 en la ecuación y despejas el tiempo t.
P(t) = 0,03t + 0.02
2,72 = 0,03t + 0.02
2,70=0,03t
t= 2,70:0,03
t=90
Quiere decir que estuvo hablando por teléfono 90 minutos lo que es equivalente a una hora y media.