Prisma y pirámide
Para resolver ejercicios y problemas sobre cálculo y demostración en prismas y pirámides, debes recordar su definición, elementos y las fórmulas para calcular su área y volumen. Además debes saber realizar demostraciones utilizando el teorema de las tres perpendiculares o su recíproco. Es por ello que te brindamos un breve resumen de estos contenidos, los que debes complementar con las propiedades de las figuras planas y sus fórmulas de área y perímetro.
Definición : Definición
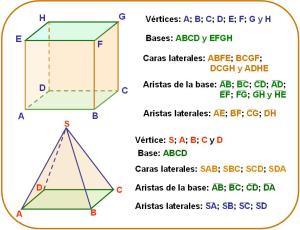
: Elementos
Recuerda que... : Fórmulas para el cálculo del volumen
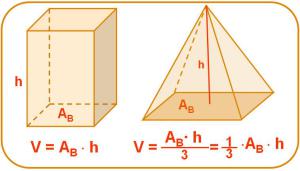
Para calcular el volumen de un prisma debes multiplicar el área de su base y su altura.
El volumen de una pirámide se calcula hallando la tercera parte de dicho producto.
Además es importante recordar que:
El área de la base se calcula aplicando la fórmula correspondiente al polígono que se encuentre en su base, por lo que es necesario recordar las fórmulas de áreas de los polígonos estudiados. Estas fórmulas las puedes encontrar en el resumen de Geometría Plana que se encuentra en los temas de Igualdad y Semejanza de triángulos.
Si el prisma es recto se puede tomar como altura cualquiera de sus aristas laterales. Si la pirámide es recta, la altura es el segmento de perpendicular trazado desde el vértice al centro de su base.
El volumen de un cuerpo se da en unidades cúbicas.
Recuerda que... : Área total y lateral
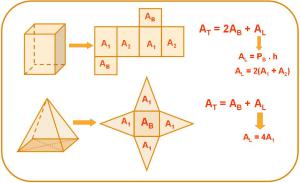
Si desarrollas ambos cuerpos sobre una superficie plana, como muestra la figura adjunta, podrás comprender que su área total se calcula adicionando las áreas de todos los polígonos que forman el cuerpo:
AT = A1 + A2 + A3 + ... + An.
- En el caso del prisma, como las bases son iguales, la fórmula se puede reducir de esta manera:
AT = 2AB + AL
El área de la base se calcula aplicando la fórmula correspondiente al polígono base del cuerpo.
El área lateral se puede calcular de dos formas:
1. Utilizando la fórmula AL = PB . h, o sea, multiplicar el perímetro de la base por la altura del prisma.
2. Adicionando las áreas de las caras laterales del prisma.
- En el caso de la pirámide, que solo tiene una base, la fórmula se escribe de esta manera:
AT = AB + AL
El área de la base se calcula aplicando la fórmula correspondiente al polígono base del cuerpo.
El área lateral se calcula adicionando las áreas de las caras laterales del prisma, que como conoces son triángulos.
- Observa un ejemplo de cómo escribir la fórmula de el área lateral, para un prisma de base rectangular y una pirámide de base cuadrada:
Paralelo al cálculo de cuerpos, es necesario también la aplicación del teorema de las tres perpendiculares para realizar demostraciones en ejercicios con estos cuerpos geométricos.
A continuación aparece este teorema, donde se destacan los elementos a considerar en la escritura de la demostración y la aplicación del teorema en sí.
Recuerda que... :
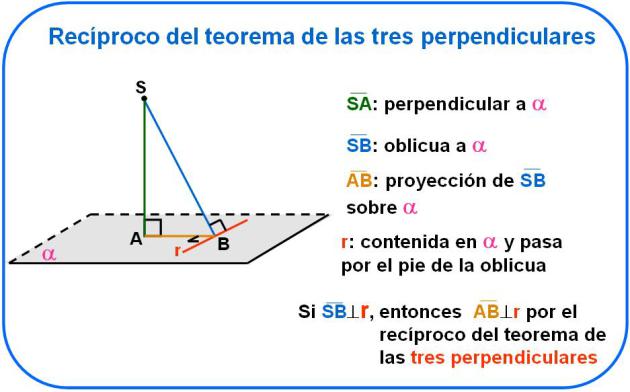
Teorema de las tres perpendiculares
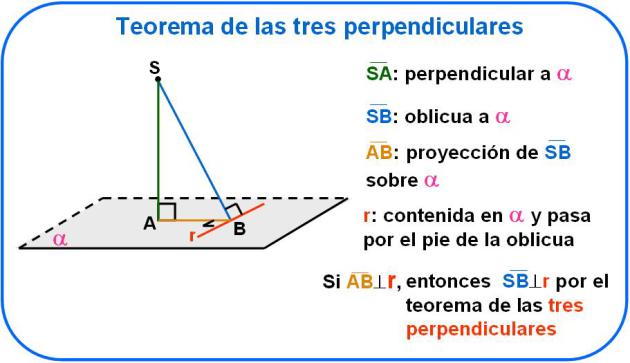
Como en otros teoremas estudiados por ti, para el teorema de las tres perpendiculares se cumple el recíproco.
En los ejemplos resueltos encontrarás ejercicios de demostración utilizando ambos teoremas y observa con atención los pasos a seguir al escribir la misma.
Debes tener en cuenta también, propiedades de la Geometría Plana relacionadas con segmentos perpendiculares que te ayudarán a argumentar por qué la proyección o la oblicua, según el caso, son perpendiculares a la recta.
Recuerda que... :
Teorema recíproco