Ejercicios resueltos
A continuación te presentamos ejercicios de cálculo y demostración en los que necesitarás aplicar las relaciones vistas con anterioridad.
: Ejercicio 1
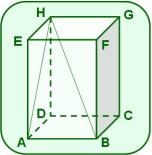
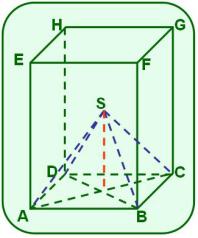
La figura muestra un prisma recto cuyas bases ABCD y EFGH son cuadrados,
es diagonal de la cara ADHE yes una de las diagonales del prisma.
a) Prueba que el es rectángulo.
b) Si = 12 dm y el , calcula el volumen del prisma.
c) Determina su área lateral.
Solución
a) Prueba que el es rectángulo.
b) Si = 12 dm y el , calcula el volumen del prisma.
Ten en cuenta que:
la base del prisma es cuadrada.
al trabajar con el teorema del ángulo de 300 y el de Pitágoras, debes declarar que el triángulo seleccionado es rectángulo.
los datos tienen dos cifras significativas, luego la respuesta debe tener también dos cifras.
como el volumen obtenido tiene en su parte entera tres cifras no es posible redondear a dos cifras, por lo tienes que cambiar de unidad de medida.
al trabajar con unidades cúbicas multiplicas o divides por potencias de mil, en este caso divides por mil, que es lo mismo que correr la coma tres lugares a la izquierda.
el cero a la izquierda no constituye una cifra significativa.
c) Determina su área lateral.
Para calcular el área lateral de un prisma puedes auxiliarte de la fórmula utilizada, pero también puedes hacerlo adicionando las áreas laterales.
Ten en cuenta que como la base es cuadrada, los cuatro rectángulos laterales son iguales y bastará con hallar el área de uno de ellos y multiplicarla por cuatro.
: Ejercicio 2
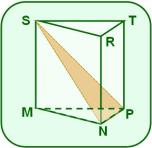
La figura muestra un prisma recto de bases triangulares MNP y SRT,
el es rectángulo en N,
y son diagonales de las caras MNRS y MPTS respectivamente.
a) Prueba que las bases del prisma son triángulos rectángulos.
b) Si ; ; y , calcula el volumen del prisma.
Solución:
a) Prueba que las bases del prisma son triángulos rectángulos.
Como por definición las bases de un prisma son iguales y paralelas, basta demostrar que una de ellas es un triángulo rectángulo.
b) Si ; ; y , calcula el volumen del prisma.
En este inciso puedes concluir que como , dicho ángulo mide 45º y el triángulo rectángulo MNP es, además, isósceles y sus catetos medirán 5 dm.
: Ejercicio 3
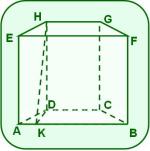
La figura muestra un prisma recto cuyas bases son los trapecios ABCD y EFGH,
K es un punto de la base mayor , tal que perpendicular a .
P(ABCD) =44,0 dm, , y el ángulo de inclinación de la oblicua con respecto al plano ABC es de 60º.
a) Probar que es una de las alturas del trapecio ABCD.
b) Halla el área lateral del prisma.
c) Calcula el volumen del cuerpo.
Solución
a) Probar que es una de las alturas del trapecio ABCD.
Para probar que es una altura basta comprobar que es perpendicular a la base mayory para ello te apoyas en el teorema de las tres perpendiculares.
b) Halla el área lateral del prisma.
Como el cuerpo es un prisma, puedes aplicar la fórmula de perímetro de la base por altura o calcular el área de los rectángulos laterales y sumarlas.
c) Calcula el volumen del cuerpo.
Ten en cuenta que para hallar el área del trapecio no necesitas saber cuánto mide cada base, pues ya conoces su suma.
: Ejercicio 4
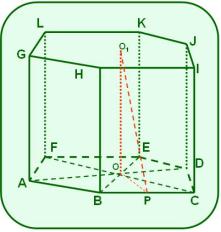
En la figura:
ABCDEFGHIJKL es un prisma recto,
sus bases son hexágonos regulares,
O es el punto de intersección de las diagonales de la base inferior,
altura del prisma,
P es un punto del lado, tal quees apotema del hexágono ABCDEF.
el perímetro del hexágono es igual a 36 dm y
a) Demuestra quees perpendicular a.
b) Calcula el volumen del prisma.
Solución
a) Demuestra quees perpendicular a.
Para resolver este inciso nos apoyamos en el teorema de las tres perpendiculares.
b) Calcula el volumen del prisma.
Para hallar el área de la base del prisma, puedes proceder de dos formas:
Al trazar las diagonales del hexágono este queda dividido en 6 triángulos equiláteros, por lo que puedes hallar el área de uno y multiplicarla por seis.
Como la base es un polígono regular, puedes utilizar la fórmula del semiperímetro por su apotema, en este caso necesitas hallar primero la apotema.
: Ejercicio 5
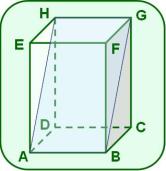
En la figura aparece representado un prisma recto de bases rectangulares.
Se conoce además que:
y son diagonales de las caras ADHE y BCGF respectivamente,
= 10,0 cm ; P(ABCD) = 28,0 cm y el = 60º.
a) Prueba que el paralelogramo ABGH es un rectángulo.
b) Calcula el área de dicho rectángulo.
c) Halla el volumen del prisma ADHBCG.
Solución
a) Prueba que el paralelogramo ABGH es un rectángulo.
Para demostrar que un paralelogramo es un rectángulo basta con probar que tiene un ángulo recto. Esto implica demostrar que la oblicuaes perpendicular a contenido en el plano ABC utilizando el teorema de las tres perpendiculares.
b) Calcula el área de dicho rectángulo.
Para hallar el área del rectángulo, debes tener la longitud de sus lados consecutivos.
c) Halla el volumen del prisma ADHBCG.
Para resolver este inciso, debes tener en cuenta la definición de prisma, para identificar correctamente las bases y su altura.
Como las bases tiene que ser iguales y paralelas, entonces para el prisma señalado las bases son los triángulos ADH y BCG, y su altura cualquiera de las aristas laterales.
: Ejercicio 6
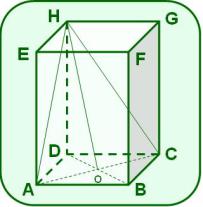
La figura muestra un prisma recto ABCDEFGH, cuyas dos bases son rombos.
O es el punto de intersección de las diagonales de la base ABCD.
y diagonales de las caras ADHE y HDCG respectivamente.
A(HAC) = 78 cm2, y .
a) Calcula el volumen del prisma.
b) Determina su área total.
Solución
a) Calcula el volumen del prisma.
Para calcular el volumen, necesitas hallar el valor de la diagonal y de la altura del prisma.
Para hallar , hay que despejar en el área del triángulo HAC tomando como altura . Sin embargo en los datos no se dice que l sea, es por eso que debes demostrarlo a partir del teorema de las tres perpendiculares o utilizando las rectas notables.
b) Determina su área total.
Para hallar el área total debes calcular:
1. el área de la base, que ya se calculó en el inciso anterior.
2. el área lateral, utilizando una de las fórmulas estudiadas. En este caso es necesario determinar la longitud del lado del rombo, lo que se puede resolver aplicando el teorema de Pitágoras.
: Ejercicio 7
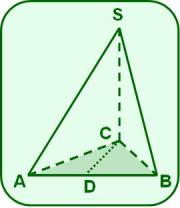
La figura muestra una pirámide de altura , es bisectriz del ángulo C y el es equilátero de 6,0 cm de lado. El ángulo de inclinación de las aristas laterales y respecto al plano de la base es igual a 60º.
a) Calcula su volumen.
b) Demuestra que la oblicua es la altura relativa a en el triángulo SAB.
Solución
a) Calcula su volumen.
Para calcular su volumen es necesario hallar el área de su base y la longitud de su altura.
b) Demuestra que la oblicua es la altura relativa a en el triángulo SAB.
Para resolver este inciso debemos apoyarnos en el teorema de las tres perpendiculares.
: Ejercicio 8
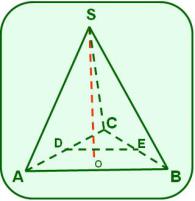
La figura muestra una pirámide recta, cuya base ABC es un triángulo equilátero y su altura es .
Se conoce además que es la paralela media del relativa al lado .
y .
Calcula el volumen de la pirámide.
Solución
Calcula el volumen de la pirámide.
Para resolver este inciso debes recordar que:
1. la paralela media de un triángulo mide la mitad de la longitud del lado que le corresponde.
2. que el centro O del triángulo es el punto de intersección de todas las rectas notables, ya que es equilátero, por lo que BA y AE son mediatrices.
: Ejercicio 9
La figura muestra una pirámide recta de base cuadrada MNPQ y altura .
O es el punto de intersección de las diagonales del cuadrado y T es el punto medio del lado .
a) Prueba que es la altura de la cara SNP de la pirámide.
b) Si el y , calcula el volumen de la pirámide.
c) Determina su área lateral.
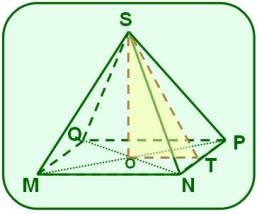
Solución
a) Prueba que es la altura de la cara SNP de la pirámide.
Para resolver este inciso, es necesario aplicar el teorema de las tres perpendiculares a partir del reconocimiento de la paralela media en la figura.
b) Si el y , calcula el volumen de la pirámide.
Para calcular el volumen es necesario hallar solo el área de la base, o sea, el área del cuadrado determinando la longitud de una de las aristas de la base.
c) Determina su área lateral.
Como la base es cuadrada y la pirámide recta, los triángulos de las caras laterales son iguales, lo que facilita su cálculo.
: Ejercicio 10
A una pirámide recta SMNPQ, de base cuadrada, se le hace un corte paralelo a su base por la tercera parte de la longitud de su altura obteniendo la pieza MNPQABCD.
La altura de la pirámide SMNPQ es y tiene una longitud de 12 cm, mientras que la diagonal del cuadrado MNPQ mide 9,0 cm.
Calcula el volumen del cuerpo resultante.
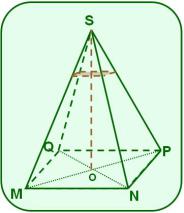
Solución:
Como el corte se hace paralelo a la base y por la tercera parte, todas las dimensiones de la pirámide SABCD tienen la tercera parte de las dimensiones de la pirámide SMNPQ.
El volumen del cuerpo resultante será igual a la diferencia de los volúmenes de ambas pirámides.
Ten en cuenta también que como la base es cuadrada y conoces la longitud de su diagonal, es más cómodo hallar su área a partir de la fórmula del área del rombo.
: Ejercicio 11
De un prisma recto de madera se quiere obtener una pirámide. Se conoce que:
Ambos cuerpos tienen igual base.
La altura de la pirámide obtenida es la mitad de la del prisma.
La altura del prisma mide 10 dm y el volumen del prisma es de 480 dm3.
a) Calcula el volumen del cuerpo resultante.
b) Determina la cantidad de madera que se desperdicia.
Solución
a) Calcula el volumen del cuerpo resultante.
La pieza resultante es la pirámide, por lo que debes hallar su volumen.
b) Determina la cantidad de madera que se desperdicia.
La cantidad de material que se desperdicia es la diferencia entre los volúmenes del prisma y la pirámide obtenida.
: Ejercicio 12
A una pirámide recta de cristal se le hará una perforación en forma de prisma recto con las siguientes características:
la base de la pirámide es un rectángulo de perímetro igual 28 cm y el lado ,
la altura de la pirámide es ,
la base del prisma es el cuadrado MNPQ y sus vértices M y P son los puntos medios de los lados del rectángulo y respectivamente,
la perforación se hizo 4,0 cm hacia adentro y M es la proyección del punto T del prisma y .
O es el punto de intersección de las diagonales del cuadrado MNPQ,
a) Prueba que es perpendicular a la diagonal del cuadrado.
b) Calcula la cantidad de cristal que se desperdicia al efectuar la perforación.
c) Halla el volumen del cuerpo resultante.
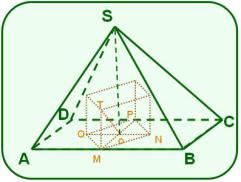
Solución
a) Prueba que es perpendicular a la diagonal del cuadrado.
b) Calcula la cantidad de cristal que se desperdicia al efectuar la perforación.
La cantidad de material que se desperdicia se corresponde con el volumen del prisma, que es la forma que tiene la perforación.
Ten en cuenta que como M y P son puntos medios de los lados y , la diagonal del cuadrado es paralela media del rectángulo y su longitud será igual a la del lado .
Como conoces las diagonales del cuadrado MNPQ, es conveniente hallar su área utilizando la fórmula para el rombo.
c) Halla el volumen del cuerpo resultante.
El cuerpo resultante es la pirámide perforada, por lo que su volumen es la diferencia de los volúmenes de la pirámide y el prisma.