EL PRISMA Y LA PIRÁMIDE

1. La figura muestra un cubo. Las diagonales de las caras ABCD, BCGF y DCGH forman el triángulo DBG cuyo perímetro es igual a $12\sqrt{2}\mathrm{cm}$.

a) Prueba que $\overline{\mathrm{GB}}\perp \overline{\mathrm{AB}}$.

Consultar^[1]

b) Calcula el volumen del cubo.

Consultar^[2]

2. La figura muestra un prisma recto cuyas bases son triángulos equiláteros, $\overline{\mathrm{AF}}$ y $\overline{\mathrm{FB}}$son diagonales de las caras ACFD y CBEF respectivamente y $\overline{\mathrm{CG}}$es la bisectriz del $\mathrm{ACB}$.

Si se sabe que el $A\left(△\mathrm{AFB}\right)=65\frac{\sqrt{3}}{3}{\mathrm{cm}}^2$ y $\overline{\mathrm{FG}}=\mathrm{13,0}\mathrm{cm}$,

a) Probar que $\overline{\mathrm{FG}}$ es la altura relativa al lado $\overline{\mathrm{AB}}$ en el $△\mathrm{AFB}$.

Consultar^[3]

b) Calcula el volumen del prisma ABCDEF.

Consultar^[4]

3. La figura muestra un prisma recto de bases triangulares. El triángulo MNP es rectángulo en N e isósceles.

a) Prueba que el triángulo SNP es rectángulo.

Consultar^[5]

b) Calcula el volumen del prisma si se conoce que $\measuredangle \mathrm{NSP}=\mathrm{30º}$ y $\overline{\mathrm{SP}}=\mathrm{12,0}\mathrm{cm}$.

Consultar^[6]

c) Determina el área lateral de dicho prisma.

Consultar^[7]

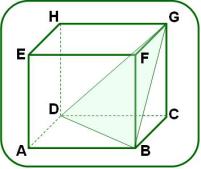
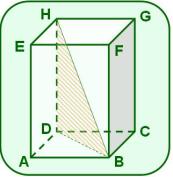
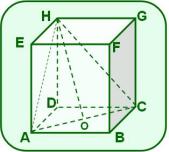
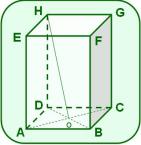
4. La figura muestra un prisma recto cuyas bases son los paralelogramos ABCD y EFGH.

• O es el punto de intersección de las diagonales $\overline{\mathrm{AC}}$ y $\overline{\mathrm{BD}}$ de la base inferior.

• $\overline{\mathrm{HO}}$ perpendicular a $\overline{\mathrm{AC}}$en el punto O.

a) Prueba que el paralelogramo ABCD es un rombo.

Consultar^[8]

b) Si el $V\left(\mathrm{ABCD}\right)=576\sqrt{3}{\mathrm{dm}}^3$, $\overline{\mathrm{HD}}=6\sqrt{3}\mathrm{dm}$ y $\overline{\mathrm{AC}}=\mathrm{16,0}\mathrm{dm}$, calcula el área lateral del prisma.

Consultar^[9]

c) Halla la amplitud del ángulo de inclinación de la oblicua $\overline{\mathrm{HO}}$ con el plano de la base ABC.

Consultar^[10]

5. En el prisma recto de la figura se conoce que:

• sus bases ABCD y EFGH son rectángulos,

• $\overline{\mathrm{DB}}=10\mathrm{dm}$, $\measuredangle \mathrm{ABD}=\mathrm{30º}$ y $\tan \left(\measuredangle \mathrm{HBD}\right)=2$.

a) Calcula el volumen del prisma.

Consultar^[11]

b) Calcula el área de la superficie rayada.

Consultar^[12]

6. La figura muestra un prisma recto de bases cuadradas ABCD y EFGH.

• $\overline{\mathrm{HA}}$ y $\overline{\mathrm{AC}}$ diagonales de las caras ADHE y DCGH respectivamente.

• O punto de intersección de las diagonales de la base inferior.

Si $A\left(△\mathrm{AHC}\right)=27\sqrt{2}{\mathrm{dm}}^2$ y $\overline{\mathrm{HO}}=\mathrm{9,00}\mathrm{dm}$, calcula el volumen del prisma.

Consultar^[13]

7. En la figura ABCDEFGH es un ortoedro, M es un punto de $\overline{\mathrm{BC}}$ tal que $\overline{\mathrm{BC}}=3\overline{\mathrm{MB}}$, $\overline{\mathrm{EB}}=\mathrm{6,0}\mathrm{cm}$, $\mathrm{sen}\measuredangle \mathrm{AEB}=\frac{\sqrt{2}}{2}$y el área rayada es igual a 24 cm².

a) Prueba que el trapecio BMHE es rectángulo.

Consultar^[14]

b) Calcula el volumen del ortoedro.

Consultar^[15]

c) Halla el perímetro del cuadrilátero BMHE.

Consultar^[16]

8. La figura muestra un prisma recto cuyas bases son los trapecios rectángulos ABFE y DCGH en B y C respectivamente,

$\tan \measuredangle \mathrm{CAB}=\mathrm{1,5}$, $\overline{\mathrm{EF}}=\mathrm{5,0}\mathrm{dm}$, $\overline{\mathrm{EA}}=\mathrm{6,0}\mathrm{dm}$ y $\overline{\mathrm{FB}}=\mathrm{9,0}\mathrm{dm}$.

a) Calcula el volumen del prisma.

Consultar^[17]

b) Determina su área lateral.

Consultar^[18]

9. La figura muestra una pirámide SABCD de base rectangular y altura $\overline{\mathrm{SD}}$.

E y F son puntos de $\overline{\mathrm{AB}}$ y $\overline{\mathrm{CD}}$respectivamente, tales que $\overline{\mathrm{EF}}\parallel \overline{\mathrm{BC}}$.

a) Probar que el $△\mathrm{SEF}$es rectángulo.

Consultar^[19]

b) Si $\overline{\mathrm{SE}}=10\mathrm{cm}$, $\overline{\mathrm{AF}}=\mathrm{6,0}\mathrm{cm}$ y $V\left(\mathrm{SEBCF}\right)=144{\mathrm{cm}}^3$, halla el volumen de la pirámide SABCD.

Consultar^[20]

10. La figura muestra una pirámide recta, cuya base es el triángulo equilátero ABC y su altura $\overline{\mathrm{SO}}$.

M y N puntos de $\overline{\mathrm{AB}}$ y $\overline{\mathrm{BC}}$, tales que $\overline{\mathrm{MN}}\parallel \overline{\mathrm{AC}}$y $A\left(△\mathrm{MNB}\right)=\mathrm{3,0}{\mathrm{cm}}^2$.

Calcula el volumen de la pirámide.

Consultar^[21]

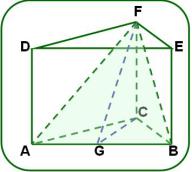
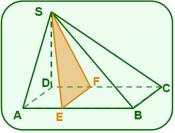
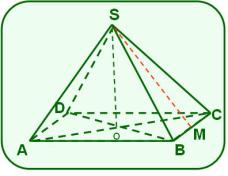
11. El área lateral de la pirámide representada es igual a 60 dm².

Se conoce además, que es recta y su altura $\overline{\mathrm{SO}}$, $\overline{\mathrm{SM}}=50\mathrm{cm}$,

B es el punto medio de la arista $\overline{\mathrm{BC}}$ y O es el punto de intersección de las diagonales del cuadrado ABCD.

a) Prueba que $\overline{\mathrm{SD}}$es la altura de la cara SBC relativa a$\overline{\mathrm{BC}}$.

Consultar^[22]

b) Calcula el volumen de la pirámide.

Consultar^[23]

12. En la figura:

- SABCD pirámide de altura $\overline{\mathrm{SA}}$y cuya base es un paralelogramo,

- O punto de intersección de las diagonales de ABCD,

- $\overline{\mathrm{SO}}$es la altura de la cara SBD,

a) Prueba que el paralelogramo ABCD es un rombo.

Consultar^[24]

b) Si $A\left(\mathrm{ABCD}\right)=12{\mathrm{dm}}^2$, $\overline{\mathrm{BD}}=\mathrm{4,0}\mathrm{dm}$ y

$\tan \mathrm{SOA}=2$, calcula el volumen de la pirámide SABD.

Consultar^[25]

13. La figura muestra un cuerpo compuesto por un cubo y una pirámide recta que tienen base común EFGH.

Se conoce además que:

• $\overline{\mathrm{SO}}$es la altura de la pirámide,

• el volumen del cubo es igual a $64{\mathrm{cm}}^3$y el $△\mathrm{SOF}$es isósceles de base $\overline{\mathrm{SF}}$.

Calcula el volumen del cuerpo.

Consultar^[26]

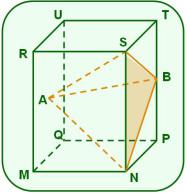
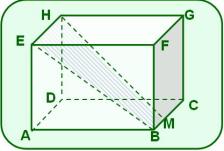
14. La figura muestra un prisma recto al que se le hace una perforación en forma de pirámide recta por una de sus caras, con las siguientes características:

• las bases del prisma son los cuadrados MNPQ y RSTU,

• A es un punto de la cara MQUR y B es un punto de la arista lateral $\overline{\mathrm{TP}}$, tal que el $△\mathrm{SNB}$ es rectángulo en B,

• $\overline{\mathrm{SB}}=\mathrm{5,0}\mathrm{dm}$ y $\overline{\mathrm{NB}}=12\mathrm{dm}$,

• el prisma tiene $A_L=132{\mathrm{dm}}^2$.

a) Determina la cantidad de material que se desperdicia al realizar la perforación.

Consultar^[27]

b) Calcula el volumen de la pieza resultante.

Consultar^[28]