FUNCIONES TRIGONOMÉTRICAS

Resuelve los ejercicios que siguen de manera independiente. Puedes consultar de nuevo las Ideas esenciales y los Ejercicios resueltos.

Cada ejercicio viene acompañado de su respuesta, para que puedas comprobar los resultados por ti obtenidos.

Compara los procedimientos que utilizaste para resolver cada uno de ellos con otros compañeros y si fuese necesario pide colaboración a tu profesor.

1. Escribe verdadero o falso según corresponda. Argumenta las falsas.

   a) ___ El gráfico de la función m cuya ecuación es m(x) = 3cos²x – 4 corta al eje de las ordenadas en el punto (0 ; – 1).

   b) ___ La función n definida en el conjunto de los números reales por la ecuación n(x) = 2sen x es una función par.

   c) ___ La correspondencia definida de R en $\left[0;1\right]$tal que a cada número real le hace corresponder el cos x es una función.

   d) ___ La función f definida por la ecuación f(x) = sen 0,5x es impar y tiene período igual 4π.

   e) ___ cos 23⁰ > cos 12⁰.

   f) ___ sen 23⁰ > sen 12⁰.

   g) ___ El valor máximo de la función q de ecuación q(x) = 3sen5x es y = 5.

   h) ___ La función p de ecuación p(x) = 3tan x tiene imagen $y\in \left(-3;3\right)$.

   Consultar^[1]

2. Dada la función g definida en el conjunto de los números reales por la ecuación g(x) = 1,5senbx.

   2.1. Marca con una X la respuesta correcta.

   a) Si el período de la función g es igual a π, entonces el valor del parámetro b es:

   ___ 1

   ___ 2

   ___ 0,5

   ___ ninguno de los anteriores.

   b) El conjunto imagen de la función g es:

   ___ $y\in ℝ$

   ___ $y\in \left(-2;2\right)$

   ___ $y\in \left(-\mathrm{1,5};\mathrm{1,5}\right)$

   ___ $y\in \left[-\mathrm{1,5};\mathrm{1,5}\right]$

   c) De la función g se puede afirmar que:

   ___ no es par ni impar

   ___ es inyectiva

   ___ uno de sus ceros es x = $\frac{\pi }{2}$

   ___ Es positiva para $\frac{\pi }{2}$< x < π

   2.2. Completa los espacios en blanco:

   a) El dominio de la función g es ____________.

   b) En el intervalo $\frac{\pi }{4}$< x < $\frac{\pi }{2}$ la función es monótona _______________.

   c) El valor mínimo de la función es __________.

   d) Al calcular g($\frac{3\pi }{2}$) se obtiene ________.

   Consultar^[2]

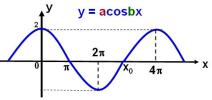
3. En el sistema de coordenadas aparece representada una función de la forma h(x) = acosbx definida en en conjunto de los números reales.

   

   3.1. Marca con una X la respuesta correcta.

   a) El valor del parámetro b es:

   ___ 1

   ___ 2

   ___ 0,5

   ___ 4

   b) La ecuación de la función h es:

   ___ h(x) = 2cos2x

   ___ h(x) = 2cos0,5x

   ___ h(x) = 2cos x

   ___ h(x) = 2cos4x

   c) El valor mínimo de la función h es:

   ___ 0

   ___ – 1

   ___ – 2

   ___ 2π

   d) La función h es decreciente y negativa para:

   ___ (0 ; π)

   ___ (π ; 2π)

   ___ (0 ; 2π)

   ___ (0 ; – 2)

   3.2. Completa los espacios en blanco.

   a) El valor de $x_0$ es _______.

   b) El valor máximo de h es ________.

   c) La imagen de h es _______________.

   d) La gráfica de la función es simétrica respecto al ________________.

   Consultar^[3]

4. Haz un esbozo de los gráficos de las funciones definidas en cada inciso por sus ecuaciones, a partir de x = 0, y hasta su período principal. Di sus propiedades en dicho intervalo.

   a) f(x) = sen2x. Consultar^[4]

   b) g(x) = 2cosx. Consultar^[5]

   c) h(x) = 1,2sen4x. Consultar^[6]

   d) t(x) = 4cos6x. Consultar^[7]

5. Sean las funciones f, g y h definidas por sus ecuaciones: f(x) = 3sen6x ; g(x) =$\sqrt{3}$tanx y h(x) =$\cos \frac{x}{2}$.

   5.1. Escribe verdadero o falso según corresponda. Argumenta las que sean falsas.

   a) ___ La función g es par.

   b) ___ La función f tiene imagen $\left\{y\in ℝ:-3\le y\le 3\right\}$.

   c) ___ La función h tiene período π.

   d) ___ La función h tiene valor mínimo y = – 1 .

   e) ___ La función g es creciente en todo su dominio.

   f) ___ El par ($\frac{\pi }{12}$; 3) pertenece a la función f.

   5.2. Completa los espacios en blanco:

   a) Al calcular f($\frac{\pi }{3}$) se obtiene ________.

   b) Al calcular g($\frac{\pi }{3}$) se obtiene ________.

   c) Al calcular h($\frac{\pi }{3}$) se obtiene ________.

   d) El período principal de la función f es _________.

   e) El conjunto imagen de la función h es __________________.

   f) Si el par ($\frac{\pi }{2}$; y) pertenece a la función h, entonces el valor de y es _______.

   Consultar^[8]

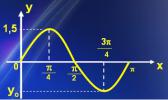
6. En la figura aparece representada una función de la forma $y=a\mathrm{sen}\mathrm{bx}$ para 0 < x < π.

   

   Marca con una X la respuesta correcta.

   a) La ecuación de la función es:

   ___ y = 1,5sen x

   ___ y = 1,5sen 2x

   ___ y = sen 2x

   ___ y = 1,5sen 4x

   b) De la función se puede afirmar que:

   ___ y_o = 1,5

   ___ es creciente y positiva para .

   ___ tiene un solo cero en el intervalo representado.

   ___ es impar.

   Consultar^[9]

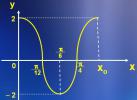
7. En la figura aparece representada una función de la forma y = acos6x para $0\le x\le x_o$.

   

   Marca con una X la respuesta correcta.

   a) El valor de x_o es:

   ___ $\frac{\pi }{3}$

   ___ $\frac{\pi }{6}$

   ___ $\frac{\pi }{2}$

   ___ $\pi$

   b) De la función se puede afirmar que:

   ___ es par.

   ___ tiene conjunto imagen $\left\{y\in ℝ:-2\le y\le 2\right\}$.

   ___ tiene valor máximo y = – 2.

   ___ es monótona.

   Consultar^[10]

8. Escribe verdadero o falso. Argumenta las falsas por qué lo son.

   a) ___ La función de ecuación y = 4tan2x es par.

   b) ___ El dominio de la función f cuya ecuación es f(x) = 5cot3x es .

   c) ___ El conjunto imagen de la función y = 2,3tanx es$\left\{y\in ℝ:-\mathrm{2,3}\le y\le \mathrm{2,3}\right\}$ .

   d) ___ La función y = cot 2x es impar.

   e) ___ La función y = – tan x es monótona decreciente.

   f) ___ Las funciones y = tan x y y = cot x no tiene máximo ni mínimo.

   Consultar.^[11]