FUNCIONES TRIGONOMÉTRICAS

Sean las funciones f, g y h definidas por sus ecuaciones f(x) = sen x ; g(x) = cos x y h(x) = tan x.

Clasifica las siguientes proposiciones en verdaderas (V) o falsas (F). De las que consideres falsas, justifica por qué lo son.

a) ___ La función g es impar.

b) ___ El dominio de la función h es el conjunto de los números reales.

c) ___ La función f es periódica.

d) ___ El conjunto imagen de la función g es $y\in \left[-1;1\right]$.

e) ___ La función h tiene máximo y = 1.

f) ___ En el intervalo 0 < x < π la función f es positiva.

g) ___ La función h es impar.

h) ___ f(π) > g(2π).

i) ___ El conjunto imagen de la función h es $y\in ℝ$.

j) ___ El período principal de la función h es 2π.

Solución:

a) Falso, porque no es simétrica respecto al origen de coordenadas o no cumple que g(– x ) = – g(x).

b) Falso, porque hay ángulos para los cuales la tangente no está definida.

c) Verdadero.

d) Verdadero.

e) Falso, porque la función tangente no tiene máximo ni mínimo.

f) Verdadero.

g) Verdadero.

h) Falso, porque f(π) = 0 y g(2π) = 1.

i) Verdadero.

j) Falso, es π, porque su gráfico se obtiene repitiendo cualquier sección de longitud igual π.

Sea la función f definida por la ecuación f(x) = 2sen4x.

Selecciona la respuesta correcta en cada inciso.

2.1. El conjunto imagen de la función f es:

a) ___ El conjunto de los números reales.

b) ___$\left\{y\in ℝ:-4\le y\le 4\right\}$

c) ___$\left\{y\in ℝ:-2\le y\le 2\right\}$

d) ___ No se puede determinar

Solución

c)$\left\{y\in ℝ:-2\le y\le 2\right\}$

La ecuación de la función tiene la forma $y=a\mathrm{sen}\mathrm{bx}$ y en este caso el valor de a representa la dilatación en el eje "y", por lo que la gráfica se proyecta sobre dicho eje de – a hasta a.

2.2. El período principal de la función f es:

a) ___ $\frac{\pi }{2}$

b) ___$\pi$

c) ___$2\pi$

d) ___ Ninguno de la anteriores.

Solución

a)$\frac{\pi }{2}$.

Recuerda que para hallarlo utilizas la fórmula $\mathrm{P.P}=\frac{2\pi }{b}$y en este caso b = 4.

2.3. De la función f se puede afirmar que:

a) ___ tiene valor máximo y = 1.

b) ___ es par.

c) ___ $f\left(\frac{\pi }{8}\right)=2$

d) ___ es negativa para 0 < x < π.

Solución

c) $f\left(\frac{\pi }{8}\right)=2$. Al sustituir en la ecuación y calcular dicho valor funcional, se obtiene 2.

El valor máximo es y = 2, ya que el parámetro a es igual a 2.

La función no es par, ya que es simétrica al origen de coordenadas y no al eje "y".

En el intervalo dado la gráfica está por encima del eje "x" de 0 a $\frac{\pi }{2}$.

Sea la función g definida por la ecuación g(x) = 3cotx.

Selecciona las afirmaciones que sean correctas.

a) ___ El dominio de la función g es $x\in ℝ$.

b) ___ El conjunto imagen de la función g es$\left\{y\in ℝ:-3\le y\le 3\right\}$.

c) ___ La función es impar.

d) ___ La función es monótona decreciente.

e) ___ El período principal de la función es 2π.

f) ___ La función no tiene máximo ni mínimo.

Solución

c) La función es impar. La función cumple que g(– x) = – g(x).

d)  La función es monótona decreciente. Al aumentar los valores del dominio disminuyen los valores respectivos de las imágenes.

f)  La función no tiene máximo ni mínimo. La gráfica es ilimitada hacia arriba y hacia abajo.

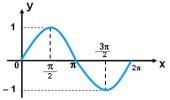
En el sistema de coordenadas rectangulares aparece representada la función f(x) = sen x definida en $x\in \left[0;2\pi \right]$.

1.1. Clasifica las siguientes proposiciones en verdaderas (V) o falsas (F). Escribe V o F en la línea dada. De las que consideres falsas, justifica por qué lo son.

a) ___ El conjunto imagen de la función f es $y\in \left(-1;1\right)$.

b) ___ La función f es creciente y negativa en el intervalo .

c) ___ La función f alcanza su valor máximo en x = $\frac{\pi }{2}$.

d) ___ El par $\left(\frac{5\pi }{3};\frac{\sqrt{3}}{2}\right)$pertenece a la función f.

1.2. Completa los espacios en blanco.

a) Los ceros de la función f en el intervalo representado son _____________________.

b) El valor mínimo de la función f es _____________.

c) Al calcular $f\left(\frac{4\pi }{3}\right)$ se obtiene _________.

Solución:

1.1.

a) Falso. Lo correcto es $y\in \left[-1;1\right]$.

b) Verdadero.

c) Verdadero.

d) Falso. Se puede argumentar de dos formas:

1. Porque para x = $\frac{5\pi }{3}$ se obtiene y = –$\frac{\sqrt{3}}{2}$.

2. Porque $\frac{5\pi }{3}$es un ángulo del cuarto cuadrante y el seno es negativo, o sea la ordenada del par tiene que ser negativa..

1.2.

a) 0 ; π; 2π.

b) y = – 1.

c) –$\frac{\sqrt{3}}{2}$.

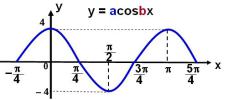
En el sistema de coordenadas aparece representada una función f definida en los reales por una ecuación de la forma $y=a\cos \mathrm{bx}$.

3.1. Marca con una X la respuesta correcta:

a) El conjunto imagen de la función f es:

___

___ $\left\{y\in ℝ\right\}$

___ $\left\{y\in ℝ:-4\le y\le 4\right\}$

___ $\left\{y\in ℝ:-1\le y\le 1\right\}$.

b) De la función f se puede afirmar que:

___ es impar.

___ tiene período principal igual π.

___ es inyectiva.

___f(0) = – 4.

c) La ecuación de la función f es:

___ y = 4cosx

___ y = 4cos2x

___ y = 4cos4x

___ y = cos4x

d) La función f es decreciente y negativa para:

___

___

___

___ $\pi \le x\le \frac{5\pi }{4}$

Solución:

3.1.

a)$\left\{y\in ℝ:-4\le y\le 4\right\}$.

b) tiene período principal igual π.

c) y = 4cos2x.

d) .

3.2. Completa los espacios en blanco.

a) El valor mínimo de la función f es ________.

b) Los ceros de la función f en el intervalo son _____________________.

c) f(π) es igual a _____.

Solución:

a) y = – 4.

b) $\frac{\pi }{4}$; $\frac{3\pi }{4}$. (Ten en cuenta que los valores extremos del intervalo no se incluyen, o sea, el intervalo es abierto)

c) 4.