Funciones trigonométricas [FUNCIONES TRIGONOMÉTRICAS]

Funciones trigonométricas

En matemática, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

De ellas es muy importante que sepas esbozar sus gráficos y determinar sus propiedades.

Ahora te mostramos un breve resumen de estos contenidos.

Función seno

Definición :

Se llama función seno a la función que a cada número real x le asocia sen x.

En otras palabras la función seno está formada por los pares ordenados (x ; sen x) con $x ∈ ℝ x in setR$ .

El gráfico y las propiedades de la función seno se presentan en el siguiente recordatorio.

Recuerda que... : Función seno. Gráfica y propiedades.

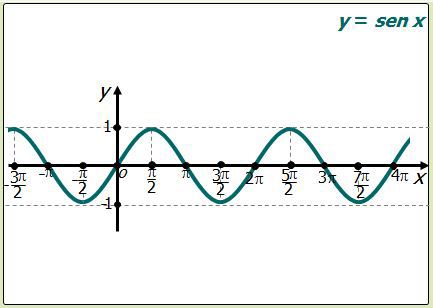
Propiedades:

Dominio: $x ∈ ℝ x in setR$ (La proyección de la gráfica cubre todo el eje "x"^[1])
Imagen: ${y ∈ ℝ : − 1 ≤ y ≤ 1} lbrace y in setR: - 1 leslant y leslant 1 rbrace$ (La proyección sobre el eje "y" cubre el intervalo de – 1 a 1^[2])
Ceros: x = kπ; $k ∈ ℤ k in setZ$ (En estos puntos la gráfica corta al eje "x"^[3])
Paridad: impar (La gráfica es simétrica respecto al origen de coordenadas o la función cumple que sen(– x) = – sen x^[4])
Monotonía: No es monótona (Se alternan intervalos de crecimiento y decrecimiento^[5])
Aunque la función seno no es monótona, en cada cuadrante si lo es, por lo que puedes recordar cómo varía su gráfica en el intervalo fundamental:
Creciente: $0; π 2 y 3 π 2; 2 π left [ 0 ; {%and} over {2} right ] y left [ {3%and} over {2}; 2%and right ]$
Decreciente: $π 2; π y π; 3 π 2 left [ {%and} over {2} ; %and right ] y left [ %and ; {3%and} over {2} right ]$
Signos: En el intervalo fundamental,
Positiva en I y II cuadrantes.
Negativa en III y IV cuadrantes.
Período: 2kπ; $k ∈ ℤ k in setZ$ .(El gráfico se obtiene "repitiendo" cualquier sección de longitud 2kπ; $k ∈ ℤ k in setZ$ ^[6])
Valor máximo y mínimo:^[7]
Valor máximo: y = 1 y lo alcanza en los puntos $x = π 2 + 2k π x = {%and} over {2}+ 2k%and$ ; $k ∈ ℤ k in setZ$ , estos son los puntos de máximo.
Valor mínimo: y = – 1 y lo alcanza $x = 3 π 2 + 2k π x = {3%and} over {2}+ 2k%and$ ; $k ∈ ℤ k in setZ$ , estos son los puntos de mínimo.

Función coseno

Al igual que la función seno, debes saber esbozar la gráfica de la función coseno y memorizar sus propiedades.

Definición :

Se llama función coseno a la función que a cada número real x le asocia cos x.

En otras palabras la función coseno está formada por los pares ordenados (x ; cos x) con $x ∈ ℝ x in setR$ .

El gráfico y las propiedades de la función coseno se presentanan en el siguiente recordatorio.

Recuerda que... : Gráfica y propiedades

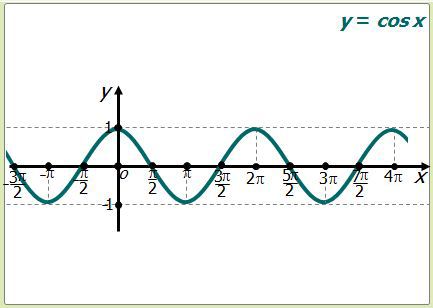
Propiedades:

Dominio: $x ∈ ℝ x in setR$ (La proyección de la gráfica cubre todo el eje "x"^[8])
Imagen: ${y ∈ ℝ : − 1 ≤ y ≤ 1} lbrace y in setR: - 1 leslant y leslant 1 rbrace$ (La proyección sobre el eje "y" cubre el intervalo de – 1 a 1^[9])
Ceros: x = (2k + 1) $π 2 {%and} over {2}$ ; $k ∈ ℤ k in setZ$ (En estos puntos la gráfica corta al eje "x"^[10])
Paridad: Par (La gráfica es simétrica respecto al eje "y" o también porque la función cumple que cos(– x) = cos x^[11])
Monotonía: No es monótona (Se alternan intervalos de crecimiento y decrecimiento^[12])
Aunque la función coseno no es monótona, en cada cuadrante si lo es, por lo que puedes recordar cómo varía su gráfica en el intervalo fundamental:
Creciente: $π; 2 π left [ %and ; 2%and right ]$
Decreciente: $0; π left [ 0 ; %and right ]$
Signos: En el intervalo fundamental,
Positiva en I y IV cuadrantes.
Negativa en II y III cuadrantes.
Período: 2kπ; $k ∈ ℤ k in setZ$ (El gráfico se obtiene "repitiendo" cualquier sección de longitud 2kπ; $k ∈ ℤ k in setZ$ ^[13])
Valor máximo y valor mínimo^[14]
Valor máximo: y = 1 y lo alcanza en los puntos x = 2kπ; $k ∈ ℤ k in setZ$ , estos son los puntos de máximo.
Valor mínimo: y = – 1 y lo alcanza x = (2k+ 1)π; $k ∈ ℤ k in setZ$ , estos son los puntos de mínimo.

Función tangente

Definición :

Se llama función tangente a la función que a cada número real x, $x ≠ (2k + 1) π 2 x <> (2k + 1){%and} over {2}$ ; $k ∈ ℤ k in setZ$ se le hace corresponder tan x.

En otras palabras la función tangente está formada por los pares ordenados (x ; tanx) con $x ∈ ℝ x in setR$ ; $x ≠ (2k + 1) π 2 x <> (2k + 1){%and} over {2}$ ; $k ∈ ℤ k in setZ$ .

Las propiedades de la tangente y su gráfico puedes verlas en el siguiente recordatorio.

Recuerda que... :

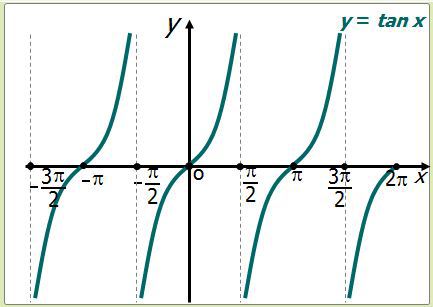
Propiedades:

Dominio: $x ∈ ℝ x in setR$ ; $x ≠ (2k + 1) π 2 x <> (2k + 1){%and} over {2}$ ; $k ∈ ℤ k in setZ$ . (La tangente no está definida en los puntos excluidos, por su lugar se trazan asíntotas^[15])
Imagen: $y ∈ ℝ y in setR$ (La proyección cubre todo el eje "x"^[16])
Ceros: x = kπ; $k ∈ ℤ k in setZ$ . (En estos puntos la gráfica corta al eje "x"^[17])
Paridad: Impar (La gráfica es simétrica respecto al origen de coordenadas, o porque la función cumple que tan(– x) = – tan x^[18])
Monotonía: No es monótona, pero es creciente en los intervalos que no contienen puntos de indefinición^[19].
Período: kπ; $k ∈ ℤ k in setZ$ (El gráfico se obtiene "repitiendo" cualquier sección de longitud kπ; $k ∈ ℤ k in setZ$ ^[20])
Valor máximo y valor mínimo^[21]
Signos: En el intervalo principal, la tangente es:
positiva: I y III cuadrantes
negativa: II y IV cuadrantes

Función cotangente

Definición :

Se llama función cotangente a la función que a cada número real x; $x ≠ k π x <> k%and$ ; $k ∈ ℤ k in setZ$ le hace corresponder cot x.

En otras palabras la función cotangente está formada por los pares ordenados (x ; cotx) con $x ∈ ℝ x in setR$ ; $x ≠ k π x <> k%and$ ; $k ∈ ℤ k in setZ$ .

Por último te presentamos el gráfico y las propiedades de la función cotangente.

Recuerda que... :

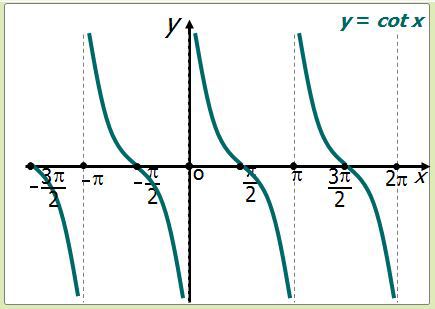
Propiedades:

Dominio: $x ∈ ℝ x in setR$ ; $x ≠ k π x <> k%and$ ; $k ∈ ℤ k in setZ$ . (La cotangente no está definida en los puntos excluidos, por su lugar se trazan asíntotas^[22])
Imagen: $y ∈ ℝ y in setR$ (La proyección cubre todo el eje "x"^[23])
Ceros: x = (2k + 1) $π 2 {%and} over {2}$ ; $k ∈ ℤ k in setZ$ . (En estos puntos la gráfica corta al eje "x"^[24])
Paridad: Impar (La gráfica es simétrica respecto al origen de coordenadas, o porque la función cumple que cot(– x) = – cot x^[25])
Monotonía: No es monótona, pero es decreciente en los intervalos que no contienen puntos de indefinición^[26].
Período: kπ; $k ∈ ℤ k in setZ$ (El gráfico se obtiene "repitiendo" cualquier sección de longitud kπ; $k ∈ ℤ k in setZ$ ^[27])
Valor máximo y valor mínimo^[28]
Signos: En el intervalo principal, la cotangente es:
positiva: I y III cuadrantes
negativa: II y IV cuadrantes

Transformaciones en las funciones seno y coseno

Además de los gráficos de las funciones trigonométricas tratadas anteriormente, también debes saber resolver ejercicios sobre gráficos y propiedades de las funciones cuyas ecuaciones tienen la forma y = asenbx y también y = acosbx.

Aquí es importante que conozcas cómo afectan a los gráficos de las funciones seno y coseno los parámetros a y b en dichas ecuaciones.

Observa un breve resumen de ellas.

Observación :

En las funciones definidas por las ecuaciones de la forma $y = a sen bx y = a sen bx$ y $y = a cos bx y = a cos bx$ :

El parámetro a representa una contracción o dilatación en el sentido del eje "y" , por lo que incide en el conjunto imagen y en los valores máximo y mínimo de la función seno y coseno.
El parámetro b: está relacionada con el período principal por la ecuación $b = 2 π P.P b={2%and} over {P.P}$ . Este parámetro representa una contracción o dilatación en el eje "x", por lo que incide en el período principal, los ceros y los intervalos de monotonía de la función.
El período principal (P.P) se puede calcular despejando en dicha expresión: $P.P = 2 π b P.P={2%and} over {b}$ .

Notas

La proyección de la gráfica cubre todo el eje "x"
La proyección sobre el eje "y" cubre el intervalo de – 1 a 1
En estos puntos la gráfica corta al eje "x"
La gráfica es simétrica respecto al origen de coordenadas o la función cumple que sen(– x) = – sen x
Se alternan intervalos de crecimiento y decrecimiento
El gráfico se obtiene "repitiendo" cualquier sección de longitud 2kπ; $k ∈ ℤ k in setZ$
Valor máximo y mínimo:
La proyección de la gráfica cubre todo el eje "x"
La proyección sobre el eje "y" cubre el intervalo de – 1 a 1
En estos puntos la gráfica corta al eje "x"
La gráfica es simétrica respecto al eje "y" o también porque la función cumple que cos(– x) = cos x
No es monótona (Se alternan intervalos de crecimiento y decrecimiento
El gráfico se obtiene "repitiendo" cualquier sección de longitud 2kπ; $k ∈ ℤ k in setZ$
Valor máximo y valor mínimo
La tangente no está definida en los puntos excluidos, por su lugar se trazan asíntotas
La proyección cubre todo el eje "x"
En estos puntos la gráfica corta al eje "x"
La gráfica es simétrica respecto al origen de coordenadas, o porque la función cumple que tan(– x) = – tan x
No es monótona, pero es creciente en los intervalos que no contienen puntos de indefinición
El gráfico se obtiene "repitiendo" cualquier sección de longitud kπ; $k ∈ ℤ k in setZ$
Valor máximo y valor mínimo
La cotangente no está definida en los puntos excluidos, por su lugar se trazan asíntotas
La proyección cubre todo el eje "x"
En estos puntos la gráfica corta al eje "x"
La gráfica es simétrica respecto al origen de coordenadas, o porque la función cumple que cot(– x) = – cot x
No es monótona, pero es decreciente en los intervalos que no contienen puntos de indefinición
El gráfico se obtiene "repitiendo" cualquier sección de longitud kπ; $k ∈ ℤ k in setZ$
Valor máximo y valor mínimo