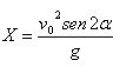Movimiento de proyectiles
Tiro parabólico
Son variados los movimientos en los cuales la trayectoria que describe el cuerpo es una parábola o una porción de esta.
El movimiento del balón de fútbol, el de la jabalina al ser lanzada, la pelota de baloncesto y otros semejantes que ocurren en nuestro planeta se clasifican como tiro parabólico.
Cualquier objeto -como balones de fútbol, pelotas de tenis, flechas y lanzas-que sea lanzado en el espacio por la acción de una fuerza se puede considerar un proyectil y el tipo de movimiento que presenta se denomina tiro parabólico.
Cualquier cuerpo lanzado y cuyo movimiento se realiza bajo la acción de la fuerza de gravedad recibe el nombre de proyectil.
Para analizar las características del tiro parabólico continuemos estudiando el movimiento de un balón pateado por un jugador.
Lanzamiento de proyectiles
¿Cómo caracterizar la posición, el desplazamiento y la velocidad del proyectil en cualquier instante de tiempo?
Analicemos este tipo de movimiento, para ello representemos el movimiento del punto material en un plano.
El cuerpo en su movimiento describe una línea curva llamada parábola, por lo tanto se requieren dos coordenadas para fijar la posición en cada instante de tiempo, ya que el movimiento se realiza en el plano X-Y.
Para su estudio, el tiro parabólico se considera como la composición de dos movimientos rectilíneos: en el eje “X” lleva un MRU y en el eje “Y”un MRUV. En la dirección del eje “X” el movimiento es MRU porque la proyección de la aceleración de la gravedad es cero y la velocidad no varía en esta dirección. En el eje “Y” la fuerza que actúa sobre el cuerpo lanzado es la fuerza de la gravedad que es una fuerza constante, por lo que el movimiento en este eje es un MRUV con aceleración constante de valor g, dirigida verticalmente hacia abajo.
Atención :
Para el estudio de los proyectiles tendremos en cuenta que sobre este solo actúa la fuerza de gravedad, aunque en la vida sobre los proyectiles actúan otras fuerzas como por ejemplo la fuerza de rozamiento del aire.
Estudio de caso : Estudio del lanzamiento de proyectiles
Supongamos que un proyectil de masa m es lanzado desde un punto O con una velocidad inicial cuya dirección forma un ángulo α con la horizontal y deseamos conocer la posición del proyectil en el espacio, así como su velocidad en cualquier instante de tiempo.
Considerando que la única fuerza que actúa sobre el proyectil es la fuerza de gravedad, la cual está dirigida verticalmente hacia abajo.
La figura representa el movimiento de un proyectil que parte del punto O situado sobre la superficie de la Tierra y que su movimiento se realiza hacia arriba. Los ejes de coordenadas se trazan atendiendo a estas condiciones.
Como el movimiento del cuerpo e gran medida depende de sus condiciones iniciales, entonces:
la velocidad inicial v0 es tangente a la trayectoria en el punto inicial y puede descomponerse en dos componentes, una vertical y otra horizontal:
Considerando que el movimiento del proyectil se produce en un plano entonces variarán dos coordenadas: una horizontal y otra vertical.
Dirección horizontal
En la dirección horizontal (x), el movimiento se comporta como rectilíneo uniforme y podemos considerarlo como MRU.
X = v0x · t = v0 (cos α) t
Donde:
X --- es la proyección del proyectil en el eje X
v0 (cos α) --- el valor de la componente de la velocidad v0x
t--- el tiempo transcurrido desde el instante t=0
Como en la dirección horizontal el movimiento es rectilíneo uniforme y este se caracteriza porque la velocidad es constante, entonces, la velocidad en cualquier instante será:
La distancia máxima alcanzada horizontalmente por el proyectil recibe el nombre de alcance.
Variando el ángulo con que se lanza el proyectil se obtiene que la mayor distancia (en el eje X) se obtiene cuando este tiene un valor de 45 0. Luego, este es el valor de ángulo idóneo para que el alcance del proyectil sea máximo.
Esto es fácilmente comprobable cuando dejamos salir agua por una manguera con diferentes ángulos de inclinación.
Dirección vertical
En la dirección vertical (Y), el cuerpo posee un movimiento rectilíneo uniformemente variado y sus ecuaciones serán:
En un instante cualquiera el módulo de la velocidad será:
y esta alcanza su máximo valor en el instante inicial O y en el punto C y el valor mínimo lo alcanza en el punto B donde la velocidad es igual:
La velocidad instantánea de un cuerpo en cualquier punto de una trayectoria curvilínea, está dirigida tangencialmente a la trayectoria en cada punto y su sentido coincide con el del movimiento en dichos puntos.
v = v0 cos α = v0x = vx
Se puede demostrar que:
El tiempo que demora el proyectil en alcanzar su máxima altura será:
la altura máxima será:
y el alcance:
