Movimiento rectilíneo uniformemente variado

Estudio de caso

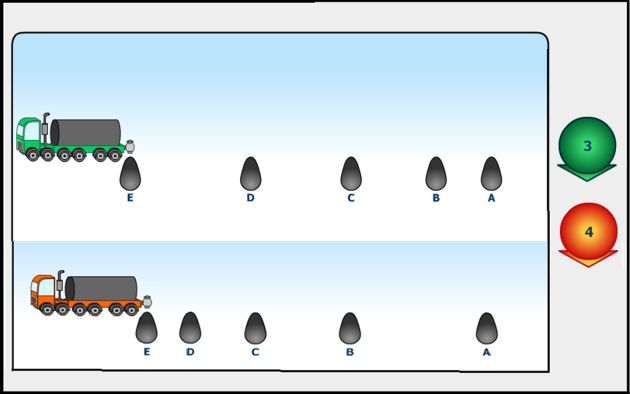
¿Cómo describir el movimiento del camión por las gotas del aceite sobre el pavimento cuando no presenta MRU?

Analiza la imagen y resuelve los siguientes ejercicios.

1. ¿Cuál es el valor de la pendiente en la gráfica correspondiente al caso 3?

a) ______10

b) ______5

c) ______20

d) ______0,5

Gráfica del movimiento del caso 3

3- Analiza la imagen y selecciona la respuesta correcta

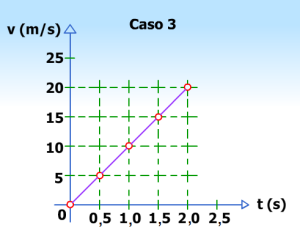
a) ______ En el caso 3 existe diferencia entre el valor de la pendiente de la gráfica del movimiento y la razón v ⃗ = Δ S ⃗ Δ t vec v`=~{%DELTA vec S } over {{%DELTA t }} .

b) ______ El camión en el caso 4 está frenando y el 3 está acelerando.

c) ______ En el movimiento del camión en el caso 3 la velocidad disminuye en el mismo valor, en iguales intervalos de tiempo.

d) ______ El camión en el caso 4 se detuvo al cabo de 2s.

e) ______ La variación de la velocidad que experimenta el camión en el caso 3 es de 5 m/s.

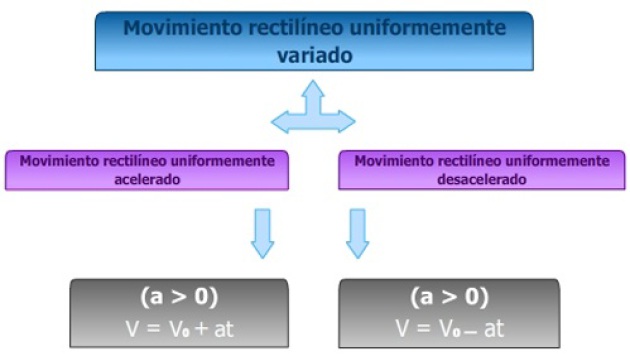
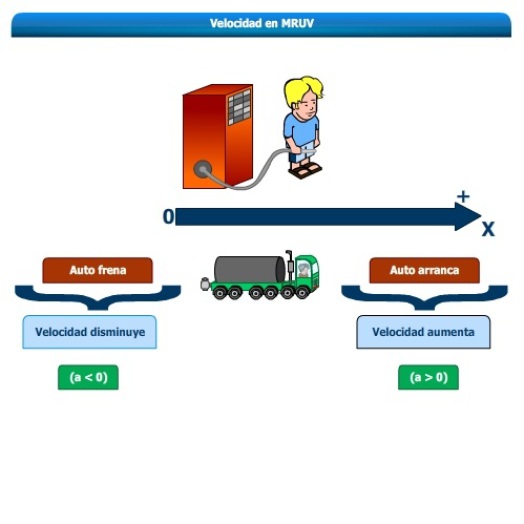
En la vida cotidiana el movimiento variado se presenta frecuentemente. Las carreras de motos, los eventos deportivos de pista, el frenado de los móviles, el inicio de nuestro camino a la escuela, son ejemplos donde se manifiesta el movimiento rectilíneo variado (MRV). Dentro de la gran diversidad de movimientos variados, el más sencillo es cuando el cuerpo sigue una trayectoria rectilínea y la velocidad experimenta iguales variaciones en intervalos iguales de tiempo. Este tipo de movimiento se denomina movimiento rectilíneo uniformemente variado (MRUV).

¿Cómo calcular la rapidez con que varía la velocidad en un movimiento rectilíneo uniformemente variado?

Si en un movimiento rectilíneo uniformemente variado se conoce que la velocidad inicial del cuerpo es y que al cabo de un intervalo de tiempo resulta igual a , entonces en cada unidad de tiempo la velocidad experimenta una variación igual a: . Esta relación caracteriza una magnitud física que se denomina aceleración.

DefiniciónAceleración

La aceleración de un cuerpo animado de un movimiento rectilíneo uniformemente variado es una magnitud física vectorial constante, que caracteriza la variación que experimenta la velocidad del cuerpo en el transcurso del tiempo en el que se produce dicha variación.

Se calcula mediante la expresión:

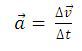
donde:

es la variación del vector velocidad y , son los vectores de las velocidades instantáneas inicial y final.

Así

a ⃗ = v ⃗ − v 0 ⃗ Δ t vec a`=~{vec v - vec v _{0} } over {%DELTA`t}

La unidad de aceleración en el SI, es el metro por segundo en cada segundo (m/s2)[1] ).

La aceleración relaciona los cambios de la velocidad con el tiempo, es decir, mide como de rápido son los cambios de la velocidad:

Si la aceleración es 0.--- la velocidad no cambia.

Si la aceleración es pequeña.--- la velocidad cambia lentamente.

Si la aceleración es grande.--- la velocidad cambia rápidamente.

La aceleración expresa como cambia la velocidad y cómo es.

Recuerda que...

La aceleración, al igual que la velocidad, es una magnitud vectorial. En este tipo de magnitudes además del valor numérico, para caracterizarla debidamente es necesario considerar su dirección y sentido. Cualquier variación que se produzca en la velocidad que lleve el cuerpo provocará aceleración en él. La dirección y sentido de la aceleración coincide con la dirección de la variación de la velocidad.

Cuando conocemos la velocidad inicial v 0 ⃗ vec v_{0} y su aceleración a ⃗ vec a , podemos determinar la velocidad instantánea en cualquier instante de tiempo. Despejando la ecuación para el cálculo de la aceleración se obtiene:

v ⃗ = v 0 ⃗ + a ⃗ ⋅ t vec v`=~vec v _{0}~+~vec a cdot t

Cuando el movimiento es uniformemente variado y el punto se desplaza por una trayectoria recta OX de forma tal que el vector es paralelo al vector , la expresión vectorial de la velocidad instantánea puede ser escrita escalarmente como:

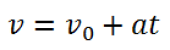
. Si v y a están dirigidos en el mismo sentido

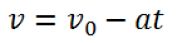
. Si y están dirigidos en sentidos contrarios .

Fundamental

La característica fundamental del MRUV es que su aceleración es constante.

La aceleración es constante cuando el cambio de velocidad en cada instante es siempre el mismo.

Los cuerpos acelerados que se mueven en línea recta, recorren diferentes desplazamientos en iguales intervalos de tiempo.

Has visto en los aeropuertos como corre un avión por una pista recta hasta que despega. Pues, parte del reposo y su velocidad va aumentando constantemente hasta que adquiere la necesaria para despegar.

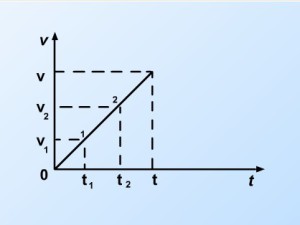
Si suponemos que el movimiento del avión es un MRUV, este movimiento puede representarse gráficamente de la siguiente forma:

Según la gráfica, el cuerpo comienza a moverse a partir del reposo y al cabo de un tiempo t alcanza la velocidad v.

Esta gráfica permite calcular la aceleración:

a = v − v 0 Δ t a`=~{v - v_{0} } over {%DELTA t}

donde:

v0 = 0

pero si tomas como referencia los puntos 1 y 2, entonces la ecuación toma la forma:

a = v 2 − v 1 t 2 − t 1 a`=~{v_{2} - v_{1} } over {t_{2} - t_{1} }

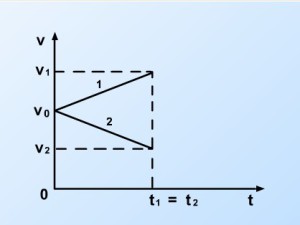
Si tenemos dos cuerpos que en el instante inicial (t = 0) poseen una velocidad inicial igual a v0 .

La gráfica 1 representa un movimiento acelerado porque la velocidad aumenta (aceleración positiva) y la 2 un movimiento retardado (aceleración negativa).

La aceleración en estas gráficas es numéricamente igual al valor de la pendiente de la recta.

La pendiente de la recta 1 es positiva, la aceleración es positiva y el movimiento es acelerado. La recta 2, la pendiente es negativa y el movimiento es retardado.

Atendiendo a si la aceleración es positiva o negativa el movimiento rectilíneo uniformemente variado se clasifica en: acelerado o retardado.

Saber más

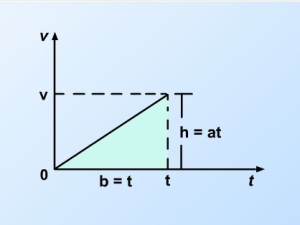
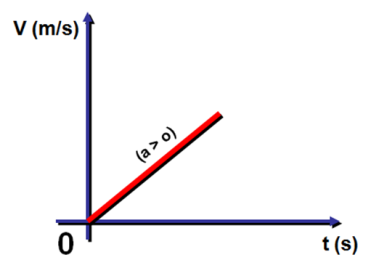
¿Qué forma adoptará la gráfica para el caso de que la velocidad inicial v0 sea igual a cero?

Si la velocidad inicial v0 es igual a cero, entonces la ecuación adopta la forma:

Y la gráfica correspondiente tiene la forma:

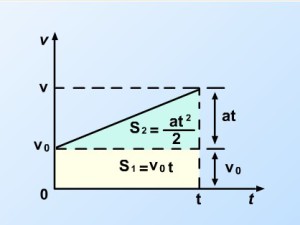
Desplazamiento en el MRUV

En este tipo de movimiento, según la gráfica, el desplazamiento es numéricamente igual al área debajo de la gráfica que está sombreada:

Δ S = a ⋅ t 2 2 %DELTA S`=~{a cdot t^{2} } over {2}

es la ecuación que permite calcular el valor del desplazamiento del cuerpo en el transcurso del tiempo cuando:

v0 = 0 y su expresión vectorial será:

Δ S ⃗ = a ⃗ ⋅ t 2 2 %DELTA vec S `=~ {vec a cdot t^{2} } over {2}

Para una velocidad inicial diferente de 0, al área del triángulo se le suma la del rectángulo y queda:

Δ S = v 0 ⋅ t + a ⋅ t 2 2 %DELTA S `=~ v _{0} cdot t +{a cdot t^{2} } over {2} que es la expresión del desplazamiento en el MRUV cuando la velocidad inicial es diferente de 0 y que vectorialmente se expresa:

Δ S ⃗ = v 0 ⃗ ⋅ t + a ⃗ ⋅ t 2 2 %DELTA vec S `=~vec v _{0} cdot t +{vec a cdot t^{2} } over {2}

La posición del cuerpo respecto al eje x en este movimiento será:

X = X 0 + Δ S X = X 0 + v 0 ⋅ t + a ⋅ t 2 2 X`=~X_{0}~+~%DELTA S newline newline ~~~~~~~~X`=~X_{0}~+~v_{0} cdot t ~+~{a cdot t^{2} } over {2}

Posición de los cuerpos que se mueven MRUV

Conociendo el desplazamiento podemos determinar la posición del cuerpo que se mueve con MRUV en cualquier instante de tiempo.

Teniendo en cuenta que la posición del cuerpo respecto al eje x se determina:

(1)

Sustituyendo la fórmula para el cálculo del desplazamiento en (1)

Teniendo en cuenta el tipo de movimiento variado, para el cálculo del valor de la posición, la ecuación anterior adopta la forma:

movimiento rectilíneo uniformemente acelerado

movimiento rectilíneo uniformemente retardado