Ejemplos resueltos
: Trayectoria de un haz de luz al incidir en un espejo
La figura representa espejos planos y rayos de luz que inciden o emergen de estos.
a) Continúa el recorrido de cada rayo de luz en las situaciones representadas.
b) ¿En qué fenómeno físico te basaste? Argumenta tu respuesta.
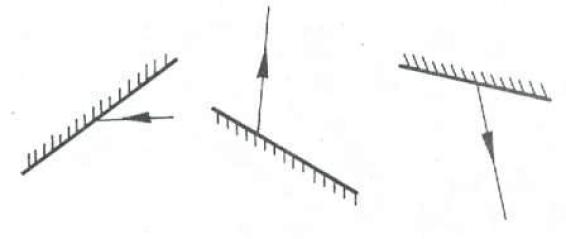
Análisis del problema
Para continuar el recorrido de los rayos de luz es preciso aplicar las leyes de la reflexión. Con el uso del semicírculo podemos garantizar que el ángulo de reflexión tenga la misma amplitud que el ángulo de incidencia.
Solución
a)
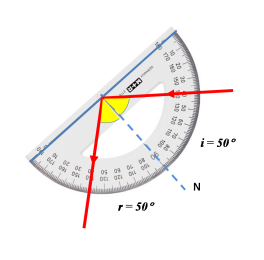
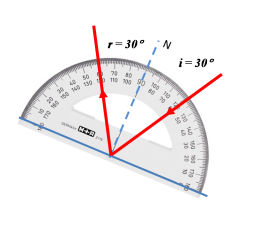
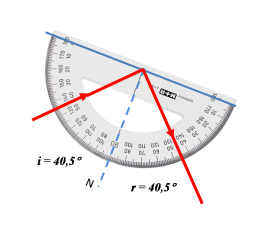
inciso b
El fenómeno es el de la reflexión de la luz. Teniendo en cuenta sus leyes: El rayo reflejado está en el plano que contiene al rayo incidente y es perpendicular al espejo y el ángulo de reflexión es igual que el ángulo de incidencia. ( i = r ), es posible continuar el recorrido de los rayos incidentes y reflejados, según corresponda.
: Formación de imágenes en espejos planos por reflexión
Localiza la posición de la imagen del objeto representado en la figura aplicando la segunda ley de la reflexión[1] y las características de las imágenes formadas en un espejo plano.

Análisis del problema
La imagen representada es un lápiz verticalmente colocado frente a un espejo plano. Localizando la posición de un punto del lápiz, en este caso su punta, y teniendo en cuenta que la imagen de un objeto frente a un espejo plano es simétrica con respecto al espejo, derecha con respecto al objeto y virtual, podemos localizar la posición del lápiz. Para esto, aplicamos la segunda ley de la reflexión al punto, situado en la punta del lápiz, por lo menos a dos de los rayos que pasan por él. En el lugar donde se corten los rayos reflejados se encuentra la imagen del punto "O". En este caso es la prolongación de estos rayos los que se interceptan en un punto. Conociendo la localización de la punta del lápiz y considerando las características de la imagen en este tipo de espejo podemos dibujar el lápiz.
Solución
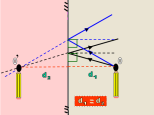
: Trazado de imágenes en espejos planos por simetría
Localiza la imagen del lápiz utilizando la propiedad de simetría.
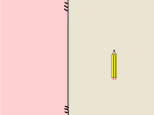
Análisis del problema
Para obtener la imagen del lápiz por simetría, podemos seleccionar dos puntos extremos del lápiz, en este caso, en la punta el "O" y en la parte de la goma el punto "A". Localizando las posiciones de las imágenes de estos puntos podemos dibujar el lápiz. Para determinar la imagen por simetría procederemos de la siguiente forma:
- trazamos una recta perpendicular al espejo que pase por el punto "O" y la prolongamos detrás del espejo (es donde se forma la imagen).
- medimos la distancia del punto al espejo, esa misma distancia es la que existe del espejo a la imagen .
De igual modo procedemos con el punto "A". Después dibujamos el cuerpo, en este caso el lápiz.
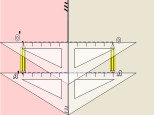
: Obtención de imágenes en los espejos cóncavos
La distancia focal (f) de un espejo esférico es la que existe entre el foco (F)del espejo y el polo del mismo.
a) Dibuja esquemáticamente un espejo cóncavo distancia focal 2 cm
b) Coloca el objeto AB frente al espejo según se orienta y determina la imagen del objeto utilizando la trayectoria de los rayos característicos.
c) ¿Cuáles son las características de la imagen obtenida?
Datos del objeto AB:
Forma:
Ubicación: Perpendicular al eje óptico principal y el punto B se encuentra sobre este.
Análisis del problema
Para obtener geométricamente la imagen de un objeto situado frente a un espejo cóncavo es necesario dibujar el espejo y tener en cuenta los siguientes elementos: el eje óptico principal[2], el polo (P), el foco (F)[3] y el centro óptico (C). Posteriormente ubicamos el objeto AB, teniendo en cuenta los datos que se ofrecen. Posteriormente se traza el objeto en la posición que corresponda, y después, utilizando los rayos notables o característicos, se determina la imagen de los puntos que conforman la imagen. Teniendo en cuenta las características del objeto y su ubicación determinamos la imagen del punto A utilizando al menos dos de los rayos característicos. En el punto donde se cortan, al menos dos de los rayos reflejados, estará la imagen del punto A, la cual se denota como A´. Como el punto B se encuentra ubicado sobre el eje óptico principal su imagen también se encuentra sobre este eje. Para trazar la imagen se tiene en cuenta que el objeto es una flecha perpendicular al eje óptico. Trazamos la flecha a partir de la ubicación de A´, en el punto donde esta se encuentra con el eje ubicamos la imagen B´. Como el objeto es una flecha, su imagen también lo es, por tal razón, la saeta la colocamos hacia el punto A´. En dependencia de la ubicación del objeto sobre eje, serán las características de la imagen que se obtiene.
Solución
inciso a)
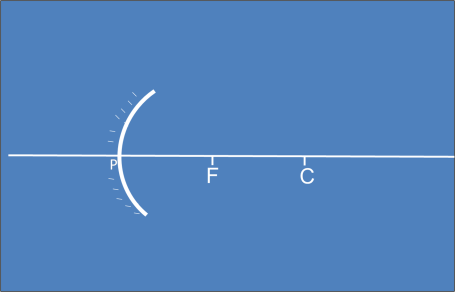
inciso b)
La solución del ejercicio dependerá de la ubicación del objeto. Tomaremos en cuenta tres posiciones y procederemos a determinar geométricamente la imagen del objeto AB.
Cuando el objeto se encuentra entre el polo (P) y el foco (F)
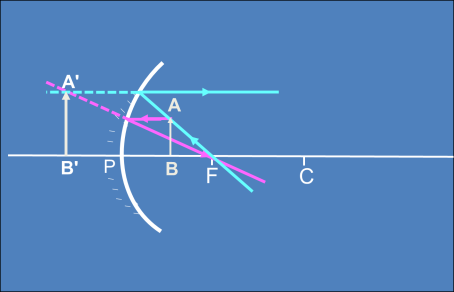
inciso c)
Característica de la imagen:
Virtual: porque se forma por las prolongaciones de los rayos reflejados.
Derecha: Tiene la misma orientación espacial.
Tiene mayor tamaño que el objeto.
Cuando el objeto se encuentra entre foco del espejo (F) y el centro óptico (C)
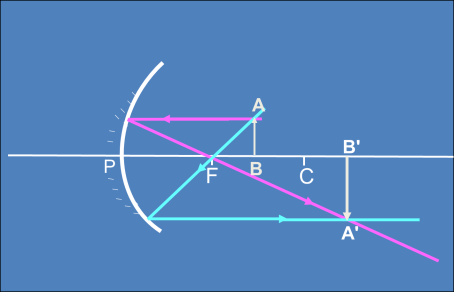
inciso c)
Característica de la imagen:
Real: porque se forma donde se cortan los propios rayos reflejados.
Invertida: No tiene la misma orientación espacial (nótese que el objeto AB está orientado hacia arriba y la imagen A´B´ lo está hacia abajo).
Tiene mayor tamaño que el objeto.
Cuando el objeto se encuentra del el centro óptico (C) hacia el infinito
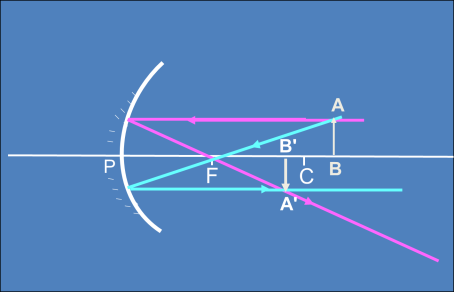
inciso c)
Característica de la imagen:
Real: porque se forma donde se cortan los propios rayos reflejados.
Invertida: No tiene la misma orientación espacial (nótese que el objeto AB está orientado hacia arriba y la imagen A´B´ lo está hacia abajo).
Tiene menor tamaño que el objeto.
: Obtención de imágenes en las lentes
Dibuja una lente convergente de distancia focal 2 cm. Sitúa un objeto AB en forma de flecha perpendicular al eje óptico principal y con uno de sus extremos sobre él a este a 5 cm de la lente. Determina la imagen de este objeto a través de un esquema utilizando los rayos característicos . Menciona las características de la imagen obtenida.
Análisis del problema
Para obtener geométricamente la imagen de un objeto situado frente a una lente convergente es necesario dibujar la lente y su eje óptico principal[2]. Como el fenómeno que se manifiesta en las lentes es el de la refracción de la luz[4] se precisa tener en cuenta que a cada lado de la lente se ubicará el foco (F)[3]. También es usual representar el punto correspondiente al doble del foco denotado como (2F). Posteriormente ubicamos el objeto AB, teniendo en cuenta los datos que se ofrecen en cuanto a forma y posición. Después, utilizando los rayos notables o característicos, se determina la imagen de los puntos que conforman la imagen. Teniendo en cuenta las características del objeto y su ubicación determinamos la imagen del punto A considerando al menos dos de los rayos característicos. En el punto donde se cortan los rayos refractados estará la imagen del punto A, la cual se denota como A´. Como el punto B se encuentra ubicado sobre el eje óptico principal su imagen también se encuentra sobre este eje. Para trazar la imagen se tiene en cuenta que el objeto es una flecha perpendicular al eje óptico. Trazamos la flecha a partir de la ubicación de A´, en el punto donde esta se encuentra con el eje ubicamos la imagen B´. Como el objeto es una flecha, su imagen también lo es, por tal razón, la saeta la colocamos hacia el punto A´. En dependencia de la ubicación del objeto sobre eje, serán las características de la imagen que se obtiene.
Solución
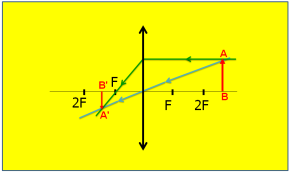
Característica de la imagen:
Real: porque se forma donde se cortan los propios rayos reflejados.
Invertida: No tiene la misma orientación espacial (nótese que el objeto AB está orientado hacia arriba y la imagen A´B´ lo está hacia abajo).
Tiene menor tamaño que el objeto.