MÉTODO GRÁFICO

Paso 1

Los vectores dados son colineales, están en la misma dirección, por lo tanto basta seleccionar un solo eje para trazarlos. Seleccionemos el eje x

Paso 2

En este ejemplo tomamos como escala:

1 cm = 1 u

Paso 3

El vector resultante $\vec{R}$ es la suma de los vectores dados, para determinarlo, apliquemos las reglas de suma de vectores colineales, teniendo en cuenta que en este caso los tres vectores tienen igual sentido.

Tracemos en el eje x los 3 vectores uno a continuación del otro, teniendo en cuenta la escala seleccionada.

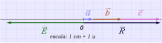
El vector $\vec{R}$ tiene su origen en el vector en $\vec{a}$ y el extremo coincide con el del vector $\vec{c}$.

Con una regla , o con ayuda del papel milimétrico , medimos la longitud de $\vec{R}$, en nuestro ejemplo:

R= 8 cm , teniendo en cuenta la escala seleccionada 8∙1= 8

R=8 u

La equilibrante $\vec{E}$es un vector que anula los efectos del vector resultante, tiene igual dirección, valor numérico , pero su sentido es contrario al del vector resultante .

$\vec{E}=-\vec{R}$

E=-8 u

Respuesta

La resultante del sistema $\vec{R}$está dirigida horizontalmente, en sentido a la derecha y tiene un valor numérico de R=8 u. El sistema de los vectores dados puede ser sustituido por cualquier vector que cumpla con estos requisitos.

La equilibrante del sistema $\vec{E}$está dirigida horizontalmente, en sentido a la izquierda y tiene un valor numérico de E=-8 u. El sistema de los vectores dados puede ser equilibrado por cualquier vector que cumpla con estos requisitos.

MÉTODO ANALÍTICO

Como los vectores se encuentran en el eje el valor de sus componentes coinciden con el valor numérico de los vectores.

Paso 1

Hallamos las componentes de los vectores

a_x= 1u

b_x= 3u

c_x= 4u

Paso 2

Determinamos la componente en el eje x del vector resultante:

R_x= a_x + b_x+ c_x

Sustituimos los valores :

R_x= 1u + 3u + 4u= 8 u

En este caso el valor numérico (módulo) del vector $\vec{R}$coincide con el valor de su componente en x

R= R_x= 8 u

Paso 3

Hallemos la equilibrante

E_x= -R_x= -8u

E = E_x = -8 u

Respuesta

El vector resultante $\vec{R}$ está dirigido horizontalmente hacia la derecha y su valor numérico:

R = R_x = 8 u

El vector equilibrante $\vec{E}$ estádirigido horizontalmente hacia la izquierda y su valor numérico:

E=E_x=-8 u

Paso 1

Los vectores dados son colineales, están en la misma dirección, por lo tanto basta seleccionar un solo eje para trazarlos. Seleccionemos el eje x

Paso 2

En este ejemplo tomamos como escala:

1 cm = 1 u

Paso 3

El vector resultante es la suma de los vectores dados, para determinarlo, apliquemos las reglas de suma de vectores colineales, teniendo en cuenta que en este caso los vectores $\vec{a}y\vec{b}$ tienen igual sentido y $\vec{c}$tiene sentido contrario a los anteriores.

Teniendo en cuenta la escala seleccionada, tracemos en el eje x los vectores $\vec{a}y\vec{b}$ uno a continuación del otro y el vector $\vec{c}$ con el origen coincidiendo con el extremo del vector $\vec{b}$.

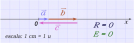
El vector $\vec{R}$ tiene su origen en el vector en $\vec{a}$ y el extremo coincide con el del vector $\vec{c}$. En este caso el origen de $\vec{a}$ coincide con el extremo de $\vec{c}$, por lo tanto el vector suma o resultante es igual al vector $\vec{0}$.

Respuesta

El sistema de vectores dado no tiene resultante , ni equilibrante. La acción del vector $\vec{c}$ equilibra a la de los vectores $\vec{a}y\vec{b}$.

MÉTODO ANALÍTICO

Como los vectores se encuentran en el eje el valor de sus componentes coinciden con el valor numérico de los vectores.

Paso 1

Hallamos las componentes de los vectores

a_x= 1u

b_x= 3u

c_x= 4u

Paso 2

Determinamos la componente en el eje x del vector resultante:

R_x= a_x + b_x+ c_x

Sustituimos los valores :

R_x= 1u + 3u + 4u = 0

Respuesta

El sistema de vectores dado no tiene resultante , ni equilibrante la acción del vector $\vec{c}$ equilibra a la de los vectores $\vec{a}y\vec{b}$.