Por el método gráfico encuentra el vector resta $\vec{c}=\vec{a}-\vec{b}$si:

a) a = 2u, $\vec{a}$ está dirigido horizontalmente en sentido a la derecha

b) b = 2u , $\vec{b}$está desfasado 60⁰ con respecto a $\vec{a}$.

MÉTODO GRÁFICO

Paso 1

Tracemos un sistema de ejes cartesianos

Paso 2

Seleccionamos una escala, en este caso tomamos:

1 cm = 2 u

Paso 3

Para determinar la resta de los vectores utilicemos el método del triángulo. Recuerda que la resta de vectores es equivalente a sumar el opuesto del segundo vector que aparece en la operación:

Con una regla y atendiendo a la escala seleccionada tracemos el vector $\vec{a}$cuyo origen coincide con el origen del sistema de coordenadas, y está dirigido en el eje en sentido positivo, desde el extremo de $\vec{a}$colocamos el origen del vector $\vec{b}$ y lo trazamos con ayuda de la regla y el transportador , teniendo en cuenta la escala y el ángulo formado con el eje x, giremos este vector en 180⁰ , para ello desde el origen de $\vec{b}$ y en la misma recta de acción traza un segmento de igual longitud pero en sentido opuesto.

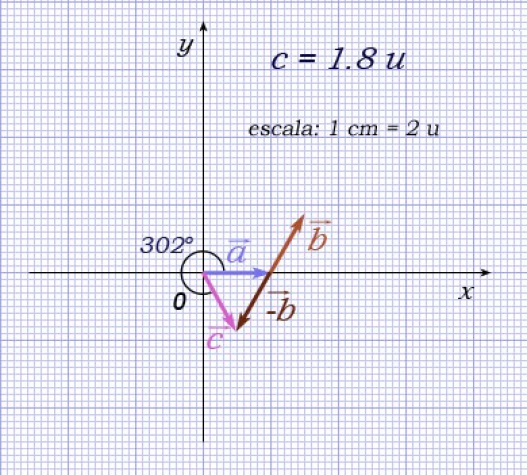
El vector resta $\vec{c}$ tiene su origen coincidente con el origen del vector $\vec{a}$ y su extremo coincide con el extremo de $-\vec{b}$.

Paso 5

Con una regla medimos la longitud de $\vec{c}$ y con el trasportador el ángulo en relación con el eje x

c=1.8 cm , teniendo en cuenta la escala seleccionada,(1.9 ∙ 1= 1.9); c=1.8 u

Para medir el ángulo coloquemos el cero del transportador coincidiendo con el punto de origen y el lado en el eje x.

θ=58⁰

Respuesta

El vector resta $\vec{c}$ ( $\vec{R}$) tiene un valor numérico igual a c=1.9 u y forma un ángulo de 58⁰ medido desde el eje de las x hasta el vector en sentido horario.

Observa que hemos restados dos vectores de igual valor numérico y a diferencia de lo aprendido en aritmética no hemos obtenido un valor 0.