Encuentra, por el método del polígono, en forma gráfica y analítica la suma de los vectores $\vec{a},\vec{b},\vec{c}y\vec{d}$, si :

a = 5u y forma un ángulo de 90⁰ con respecto a la horizontal , en sentido positivo (hacia arriba ).

b = 15u y forma un ángulo de 40⁰ con respecto a la horizontal , en sentido positivo ( hacia la derecha ).

c= 25u y forma un ángulo de 0⁰ con respecto a la horizontal , en sentido positivo ( hacia la derecha ).

d = 10u y forma un ángulo de 240⁰ con respecto a la horizontal , en sentido negativo ( hacia izquierda ).

MÉTODO GRÁFICO

Paso 1

Tracemos un sistema de ejes cartesianos

Paso 2

Seleccionamos una escala, en este caso tomamos:

1 cm = 5 u

Paso 3

Para determinar la suma de los vectores utilicemos el método del polígono. Tomemos como base al vector $\vec{a}$.

Con una regla y atendiendo a la escala seleccionada tracemos el vector $\vec{a}$ ,cuyo origen coincide con el origen del sistema de coordenadas, y está dirigido en el eje en sentido positivo, desde el extremo de $\vec{a}$ colocamos el origen del vector $\vec{b}$ y lo trazamos con ayuda de la regla y el transportador, teniendo en cuenta la escala y el ángulo formado con el eje x, de igual manera trazamos los vectores $\vec{c}$ y $\vec{d}$, colocando el origen de $\vec{c}$en el extremo de $\vec{b}$y el de $\vec{d}$en el extremo de $\vec{c}$.

El vector suma $\vec{R}$ tiene su origen coincidente con el origen del vector $\vec{E}$ y su extremo coincide con el extremo de$\vec{d}$.

Paso 4

Con una regla medimos la longitud de $\vec{R}$ y con el trasportador el ángulo entre $\vec{R}$y el eje x

R=6.4 cm , teniendo en cuenta la escala seleccionada, (6.4 ∙ 5=32) R=32 u

Para medir el ángulo coloquemos el cero del transportador coincidiendo con el punto de origen y el lado en el eje x.

φ=10⁰

Respuesta

El vector suma $\vec{R}$ tiene un valor numérico igual a R= 32u y forma un ángulo de 10⁰ con relación al eje positivo de las x

MÉTODO ANALÍTICO

Utilizamos el método de las componentes

Paso 1

Hallamos el valor de las componentes de los vectores $\vec{a},\vec{b},\vec{c}y\vec{d}$

a_x= a cos⁡ α ; a_y=a sen⁡α

a_x= 5 cos⁡ 90⁰ = 0; ya que cos⁡ 90⁰ = 0

a_y= 5; ya que sen⁡ 90⁰ = 1

b_x= b cos⁡ β; b_y= b sen β

b_x= 15 cos⁡40⁰ = 11.49, ya que cos ⁡40⁰ = 0.76

b_y= 15 sen⁡40⁰ = 9.64; ya que sen ⁡40⁰ = 0.64

c_x= c cos⁡ δ; c_y= c sen δ

c_x= 25 cos⁡ 0⁰ = 25, ya que cos ⁡0⁰=1

c_y= 0, ya que sen ⁡0⁰ = 0

d_x= d cos ⁡θ; d_y= d sen θ

d_x= 10 cos⁡240⁰ = -5 cos⁡240⁰ = -0.5

d_y= 10 sen240⁰ = -8.6 sen ⁡240⁰ = -0.86

Paso 2

Hallamos las componentes del vector $\vec{R}$

R_x= a_x + b_x+ c_x + d_x= 0 + 11.49 + 25-5 = 31.49

R_y= a_y + b_y + c_y + d_y= 5 + 9.64 + 0-8.6 = 6.04

Paso 3

Hallamos el valor numérico de $\vec{R}$

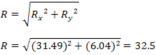
Paso 4

Para determinar el ángulo entre $\vec{R}$ y el eje x, calculemos la tangente del ángulo β

Paso 5

Sustituyendo los valores

Con una calculadora científica hallamos el valor del ángulo correspondiente a esta tangente.

φ= 10.8⁰

Respuesta

El vector suma $\vec{R}$ tiene un valor numérico igual a R=32.5 u y forma un ángulo de 10.8⁰con relación al eje positivo de las x.

Como se observa hay pequeñas discrepancias entre los valores obtenidos por el método gráfico y el analítico relacionadas con errores asociados al proceso de medición.