Magnitudes directas e indirectas. Incertidumbre en la medición

Sabemos que la física es una ciencia natural en tanto se ocupa del estudio de sistemas y fenómenos relativos a la naturaleza y que es una ciencia exacta, en tanto para la explicación de los sistemas y las predicciones de su comportamiento utiliza modelos matemáticos y que en consecuencia tiene un elevado nivel teórico. Por otra parte, también que tiene un carácter marcadamente experimental.

Las mediciones pueden ser: directas o indirectas

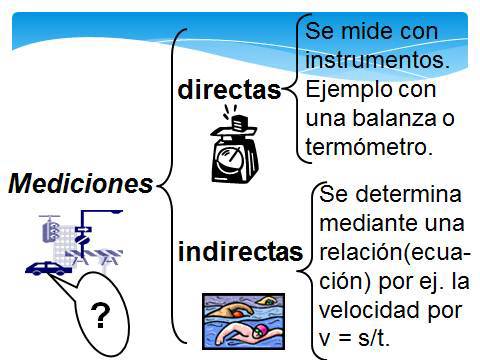
Profundicemos en las mediciones directas.

Ejemplo: La masa de una varilla de plomo puede ser determinada con una balanza, el tiempo que debe ser calentada cierta cantidad de líquido para qué alcance la temperatura de 70°C, puede ser controlado mediante su medición con un cronómetro. Estas dos situaciones constituyen mediciones directas.

Si no es posible encontrar un procedimiento experimental para realizar la medición de una magnitud físicas utilizando solamente instrumentos de medición, se recurre entonces a las mediciones indirectas.

Este tipo de mediciones se caracteriza por:

Ejemplo: La densidad de una sustancia líquida puede ser medida directamente con un densímetro (fig. 2.1). Pero si la sustancia es sólida es necesario proceder de otro modo.

En este último caso, si se dispone de una balanza y una probeta, la masa del cuerpo y su volumen pueden ser determinados de forma directa. Conocidos estos valores, la densidad (que se simboliza por la letra griega ρ ) se puede calcular mediante la expresión:

La densidad, en este caso, se ha medido de forma indirecta y la ecuación utilizada recibe el nombre de función de la medición.

Para calcular el valor de una medición indirecta, una vez realizadas las mediciones directas pertinentes, es posible utilizar dos métodos: el analítico y el gráfico.

En el método analítico se obtiene el valor al sustituir los datos en la función de la medición y en el método gráfico el valor se obtiene a partir del gráfico de la función de la medición.

Toda medición está afectada por factores que provocan alteraciones que impiden obtener el valor verdadero de la magnitud, pero tampoco es posible conocerlos todos ni en cuánto afectan la medición. Esta situación provoca una duda acerca de la validez del valor que se obtiene al realizar una medición y el Vocabulario Internacional de Metrología (VIM) establece el término incertidumbre para denominarla.

La Guía para Medición de la Incertidumbre de la Medición (GUM) establece los procedimientos con los que puede ser estimada cuantitativamente la duda, ofreciendo con ello criterios de valoración del resultado de la medición obtenido.

Para evidenciar esto, de manera rápida, se puede hacer lo siguiente: haga al menos cinco mediciones del tiempo que demoran 80 de sus pulsaciones con un reloj cuya resolución tenga un valor no mayor que un segundo.

Lo más probable es que al comparar los valores obtenidos no todos sean iguales. Ello es una fuente de la duda llamada incertidumbre. Las preguntas inmediatas son: ¿cuál de los valores obtenidos será el que se debe declarar como resultado de la medición?, ¿cómo estimar el valor de la duda? Los epígrafes que siguen ayudarán a encontrar, en buena medida, las respuestas.

Es importante no confundir los términos incertidumbre y error. El error es la diferencia entre el valor medido y el valor verdadero y no es posible calcularlo, mientras que la incertidumbre es la cuantificación de la duda acerca del valor medido que sí es posible estimar.

Puede ser conveniente señalar que comprender bien que la medición de una magnitud siempre tiene una cierta incertidumbre es algo esencial y que los métodos para poder calcular dichas incertidumbres son tan importantes para la ciencia que constituyen un objeto especial de estudio. Sin embargo el conocimiento específico de estos métodos, que pueden resultar muy complejos, es algo propio de especialistas.

A los fines de los no especialistas en este campo resulta suficiente poder determinar las cotas superiores de la incertidumbre (que en lo adelante llamaremos simplemente incertidumbre) al medir una magnitud, mediante procedimientos relativamente sencillos, que es lo que trataremos de hacer a continuación.

A los fines de los no especialistas en este campo resulta suficiente poder determinar las cotas superiores de la incertidumbre (que en lo adelante llamaremos simplemente incertidumbre) al medir una magnitud, mediante procedimientos relativamente sencillos, que es lo que trataremos de hacer a continuación.

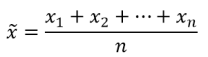
En ocasiones no tiene sentido realizar varias mediciones, pues su valor no cambia, por ejemplo, si medimos el largo un de listón de madera con una cinta métrica. En otros casos, si es conveniente realizar varias mediciones, por ejemplo, si medimos el diámetro de una moneda con un micrómetro que puede apreciar hasta las décimas de milímetro (¿Por qué en este caso es conveniente hacer varias mediciones?).

Medición del diámetro de una moneda

El valor medio para la masa de ese cuerpo, calculado sumando todos los valores y dividiendo el resultado por 10, es de 34,1 g.

Pero no es suficiente haber encontrado el valor más representativo que será el que se reporte en una medición, es necesario además caracterizar la desviación de los valores medidos del valor medio porque ello ofrece información acerca de la calidad de la medición y es premisa para la estimación de la incertidumbre.

En la incertidumbre influye tanto el instrumento de medición utilizado como el propio proceso de medición (método utilizado, fluctuaciones de las condiciones ambientales, habilidades del experimentador y otros).

Si la mayor influencia está dada por el instrumento de medición, se puede reportar como incertidumbre la menor división de la escala del instrumento en cuestión. Por ejemplo, si al medir la masa del cuerpo indicado la balanza utilizada permite apreciar hasta 0,1 g, entonces la incertidumbre en la medición tendrá ese mismo valor y podemos escribir que la masa del cuerpo es:

m=34,1 ± 0,1 g

En el caso de que la mayor influencia sea del segundo tipo se puede estimar la incertidumbre de la medición de la forma siguiente:

1) Se halla el módulo de la desviación de cada medida respeto al valor medio:

2) Se calcula la incertidumbre media de la forma siguiente:

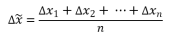
Esta ecuación nos indica que la medición del valor de x está entre:

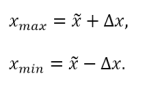
Esto nos indica que el valor más probable de la magnitud x esta entre x_max y x_(min )

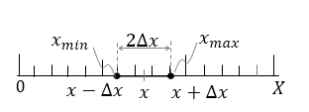
¿Es una medición buena o mala?

Una incertidumbre de 0,5 m puede parecer muy grande si medimos la longitud del aula, pero si medimos la longitud de la escuela, será pequeña respecto a esta. Por lo tanto, necesitamos estimar la incertidumbre relativa de la medición. Esta incertidumbre relativa, que denominaremos Δx_relse define mediante la ecuación:

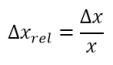
donde ∆x es la incertidumbre absoluta de la medición x.

La incertidumbre relativa se acostumbra a expresar en “por ciento”. A estos efectos basta con multiplicar por 100 el resultado obtenido. Por ejemplo si para una medición la incertidumbre relativa es de 0,20, se puede decir que esta es del 20%.