Glosario [Sistematización sobre funciones]

Glosario

a lo sumo: La expresión a lo sumo, significa que no existe mas de la cantidad indicada , pero pueden ser menos .
Ejemplo
A la reunión deben asistir a lo sumo dos personas
Quiere decir que solo pueden asistir hasta dos personas no más , pero puede ir una.
al menos: La expresión al menos significas una cantidad mínima, pero pueden ser más
Ejemplo
Deben asistir a la reunión o mitin al menos tres personas .
Significa que el mínimo de personas que deben asistir es tres , pueden ser más.
ceros: Los ceros de una función son los elementos del conjunto dominio que anulan a dicha función, simbólicamente f(x) =0.
Conjunto imagen de una función: En la función , al subconjunto de B formado por los valores para cada se llama conjunto imagen de la función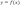
creciente: Una función es creciente en un intervalo, si al aumentar los valores de la variable independiente , aumentan los valores de la variable dependiente .

decreciente: Una función es decreciente en un intervalo, si al aumentar los valores de la variable independiente , disminuyen los valores de la variable dependiente .
dominio: El dominio de una función es el conjuntos de valores que puede tomar la variable independiente par que la función esté definida.
eje de las ordenadas: En un sistema de coordenadas se llama eje de las ordenadas a la recta vertical, donde se representan los valores de la variable dependiente.

función: Función es la relación entre dos conjuntos, llamados dominio e imagen que se establece de forma tal que a cada elemento del dominio le corresponde un único elemento del conjunto imagen.
función par: Es la función para la que se cumple que:
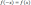, para todo elemento de su dominio.
Es estos casos se dice que la función presenta paridad par.
Geométricamente se dice que una función es par si su gráfico es simétrico respecto al eje de las ordenadas (eje ).
imagen: Valor que se obtiene al aplicar la función y=f(x) a un elemento del dominio de dicha función.

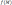máximo de una función: Una función tiene su valor máximo en si cumple que:
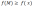, siendo cualquier elemento del dominio de .
Este se conoce como máximo absoluto ya que también se pueden encontrar valores máximos para determinados intervalos de la función.
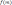mínimo de una función: Una función tiene su valor mínimo en si cumple que:
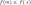siendo cualquier elemento del dominio de .
Este se conoce como mínimo absoluto ya que también se pueden encontrar valores mínimos para determinados intervalos de la función.
No positiva: Esta expresión indica el conjunto de valores negativos e incluye al cero
par ordenado: Una pareja ordenada (o un par ordenado) es un par de números reales que se escriben entre paréntesis, separados por una coma y en un único orden.
Cada número real se llama componente del par y se distingue una primera componente correspondiente al eje de las abscisas y una segunda componente referida al eje de las ordenadas.
De manera general se habla de los pares ordenados de la forma (x,y).
Son ejemplos de pares ordenados: (2,5) y (1.5,3.6).