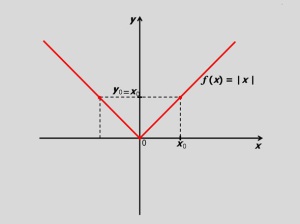
Función modular . Propiedades [Función modular]

Función modular . Propiedades

Para referirnos a la función modular o de valor absoluto se debe ver primero la imagen

Recuerda que... :

Se define como valor absoluto o módulo de un número real a, que denotamos |a|, como: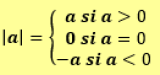

Meditar :

Fundamentada en la definición que ya conoces sobre módulo o valor absoluto se pueden establecer relaciones entre las magnitudes que intervienen y estudiar como otra de las funciones la función modular

¿ Qué características tienen las funciones modulares?

La función modular se puede identificar por la ecuación $f (x) = ∣ x ∣ f(x)= lline x rline$ . Atendiendo a las condiciones del módulo^[1] se puede afirmar que :

Si $x ≥ 0 x geslant 0$ se tiene que $∣ x ∣ = x lline x rline = x$ que es equivalente a plantear $y = x y = x$ por lo que la gráfica coincide con la recta que biseca al primer cuadrante.

Si $x < 0 x < 0$ entonces $∣ x ∣ = − x lline x rline = %menos x$ que es equivalente a plantear $y = − x y = %menos x$ por lo que la gráfica coincide con la recta que biseca al segundo cuadrante.

Con este análisis podrás comprender, el por qué del comportamiento de la gráfica de la función modular.

Propiedades de una función modular

En toda función modular es posible analizar:

Dominio e imagen

Ceros

Signos

Monotonía

Paridad

Como las otras funciones estudiadas, la función modular también puede desplazarse en sentido positivo o negativo respecto al eje de las ordenadas^[2] o al eje de las abscisas.^[3] La ecuación en estos casos es $f (x) = ∣ x + d ∣ + e f(x)= lline x+d rline + e$ , en la que el desplazamiento en el eje de las x corresponde a -d y en el eje de las y al valor de e respecto a la función de la forma $f (x) = ∣ x ∣ f(x)= lline x rline$ .

Desplazamiento en ambos sentidos es decir sobre el eje de las abscisa y sobre el eje de las ordenadas

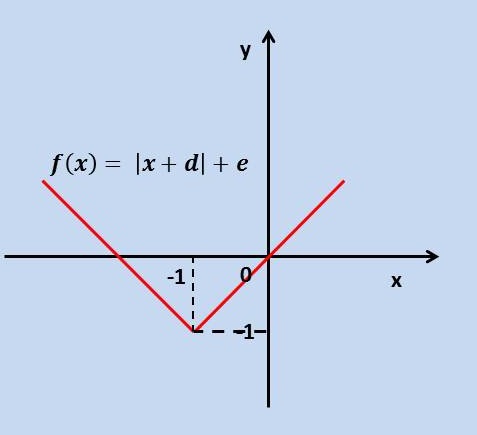
El análisis de estas propiedades^[4] se realiza de forma análoga a las funciones ya estudiadas, excepto el procedimiento para determinar el cero de la función que verás a continuación.

Saber hacer : ¿Cómo determinar los ceros de una función modular?

Para determinar los ceros de la función $g (x) = ∣ x − 1 ∣ − 4 g(x)= lline x %menos 1 rline%menos 4$ se procede de la siguiente forma:

Se iguala la función a cero

$0 = ∣ x − 1 ∣ − 4 0 = lline x %menos 1 rline%menos 4$

Se consideran las condiciones para el argumento del módulo por separado, se despeja y calcula el valor de la variable:

Para $x − 1 ≥ 0 x %menos 1 geslant 0$	Para $x − 1 < 0 x %menos 1 < 0$
El argumento del módulo se mantiene y se obtiene: $x − 1 − 4 = 0 x %menos 1%menos 4 = 0$ de donde $x − 5 = 0 x %menos 5 = 0$ por lo que obtiene como un cero a $x = 5 x = 5$	El argumento del módulo cambia de signo y nos queda: $− x + 1 − 4 = 0 %menos x+ 1%menos 4 = 0$ se obtiene que el otro cero es $x = − 3 x = %menos 3$

Para $x − 1 ≥ 0 x %menos 1 geslant 0$

Para $x − 1 < 0 x %menos 1 < 0$

El argumento del módulo se mantiene y se obtiene:

$x − 1 − 4 = 0 x %menos 1%menos 4 = 0$ de donde

$x − 5 = 0 x %menos 5 = 0$ por lo que obtiene como un cero a

$x = 5 x = 5$

El argumento del módulo cambia de signo y nos queda:

$− x + 1 − 4 = 0 %menos x+ 1%menos 4 = 0$ se obtiene que el otro cero es

$x = − 3 x = %menos 3$

Esto quiere decir que lo los dos ceros de la función son x = 5 y x= -3

Conocidas las propiedades de la función modular y las características de su gráfica te sugiero realizar los siguientes ejercicios para que apliques lo aprendido.